题目内容
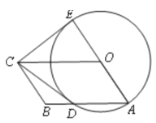
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长 AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若平行四边形OABC的两边长是方程![]() 的两根,求平行四边形OABC的面积.
的两根,求平行四边形OABC的面积.
【答案】(1)、证明过程见解析;(2)、48.
【解析】
试题分析:(1)、连接OD,根据切线得出∠OEC=90°,根据OD=OA以及OC∥AD得出∠OAD=∠EOC,则∠EOC=∠DOC,结合OD=OE,OC=OC得出△ODC和△OEC全等,从而得出∠ODC=∠OEC=90°,得出切线;(2)、根据方程得出OC=10,OA=6,根据勾股定理得出CD=8,根据全等得出CE=8,然后计算四边形的面积.
试题解析:(1)、连OD,∵CE是⊙O的切线, ∠OEC=90O ,∵OD=OA,∴∠ODA=∠OAD,又∵OC//AD
∴∠OAD =∠EOC,∠DOC=∠ODA,∴∠EOC=∠DOC, 又∵OD=OE,OC=OC, ∴△ODC≌△OEC(SAS)
∴∠ODC=∠OEC=90 O, ∴CD是⊙O的切线。
(2)、![]() ,
,![]() ,即OC=10,OA=6 在Rt△ODC, CD=8 ∵△ODC≌△OEC ,CE=CD=8
,即OC=10,OA=6 在Rt△ODC, CD=8 ∵△ODC≌△OEC ,CE=CD=8
∴平行四边形OABC的面积S=OA×CE=6×8=48

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目