Question

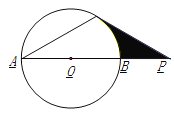
【题目】如图甲所示，是小亮设计的一种智力拼图玩具的一部分，已知AB∥CD，∠B=30°，∠BEC=62°，求∠C的度数．
（1）填写根据：过点E作EF∥AB，如图甲所示， ∵AB∥DC，EF∥AB，
∴EF∥DC（）
∴∠B=∠BEF（）
∠C=∠CEF（）
∴∠B+∠C=∠BEF+∠CEF
即∠B+∠C=∠BEC
∴∠C=∠BEC﹣∠B=62°﹣30°=32°
（2）方法迁移：如图乙，已知AE∥CD，若∠DCB=135°，∠ABC=72°，试求∠BAE的度数．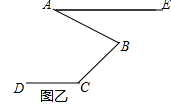

Answer 1

【答案】
（1）两条直线都与第三条直线平行，那么这两条直线平行；两直线平行，内错角相等；两直线平行，内错角相等
（2）解：如图，过B作BF∥AE，

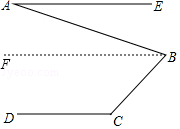
∵AE∥CD，

∴BF∥CD，

∴∠DCB+∠CBF=180°，∠BAE=∠ABF，

∵∠DCB=135°，

∴∠CBF=180°﹣135°=45°，

∵∠ABC=72°，

∴∠ABF=∠ABC﹣∠CBF=72°﹣45°=27°，

∴∠BAE=27°

【解析】解：（1）∵AB∥DC，EF∥AB， ∴EF∥DC（两条直线都与第三条直线平行，那么这两条直线平行 ）
∴∠B=∠BEF（ 两直线平行，内错角相等）
∠C=∠CEF（ 两直线平行，内错角相等 ）
∴∠B+∠C=∠BEF+∠CEF
即∠B+∠C=∠BEC
∴∠C=∠BEC﹣∠B=62°﹣30°=32°；
所以答案是：两条直线都与第三条直线平行，那么这两条直线平行； 两直线平行，内错角相等； 两直线平行，内错角相等．
【考点精析】认真审题，首先需要了解平行线的判定与性质(由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质)．