题目内容
设a<b<c<d,如果x=(a+b)(c+d),y=(a+c)(b+d),z=(a+d)(b+c),那么x、y、z的大小关系为
- A.x<y<z
- B.y<z<x
- C.z<x<y
- D.不能确定
A
分析:比较x、y、z的大小,只需判断x-y、y-z的符号.进一步将已知中x=(a+b)(c+d)、y=(a+c)(b+d)、z=(a+d)(b+c)代入化简,根据a<b<c<d来判断代数式的符号即可.
解答:∵a<b<c<d,
a-b<0,a-c<0,a-d<0,b-c<0,b-d<0,c-d<0,
∵x=(a+b)(c+d),y=(a+c)(b+d),z=(a+d)(b+c),
∴x-y=(a+b)(c+d)-(a+c)(b+d),
=ac+ad+bc+bd-ab-ad-bc-cd,
=ac+bd-ab-cd,
=(ac-cd)+(bd-ab),
=c(a-d)-b(a-d),
=(a-d)(c-b)<0,
y-z=(a+c)(b+d)-(a+d)(b+c),
=ab+ad+bc+cd-ab-ac-bd-cd,
=ad+bc-ac-bd,
=(ad-bd)+(bc-ac),
=(a-b)(d-c)<0,
∴x-y<0,y-z<0,即x<y,y<z,
∴x<y<z.
故选A.
点评:本题考查了因式分解,解决本题的关键是通过作差比较,这是一种常用的比较大小的方法.
分析:比较x、y、z的大小,只需判断x-y、y-z的符号.进一步将已知中x=(a+b)(c+d)、y=(a+c)(b+d)、z=(a+d)(b+c)代入化简,根据a<b<c<d来判断代数式的符号即可.
解答:∵a<b<c<d,
a-b<0,a-c<0,a-d<0,b-c<0,b-d<0,c-d<0,
∵x=(a+b)(c+d),y=(a+c)(b+d),z=(a+d)(b+c),
∴x-y=(a+b)(c+d)-(a+c)(b+d),
=ac+ad+bc+bd-ab-ad-bc-cd,
=ac+bd-ab-cd,
=(ac-cd)+(bd-ab),
=c(a-d)-b(a-d),
=(a-d)(c-b)<0,
y-z=(a+c)(b+d)-(a+d)(b+c),
=ab+ad+bc+cd-ab-ac-bd-cd,
=ad+bc-ac-bd,
=(ad-bd)+(bc-ac),
=(a-b)(d-c)<0,
∴x-y<0,y-z<0,即x<y,y<z,
∴x<y<z.
故选A.
点评:本题考查了因式分解,解决本题的关键是通过作差比较,这是一种常用的比较大小的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
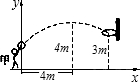 永嘉县九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
永嘉县九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
 某杂技团用66米的幕布围成一个矩形临时场地,并留出2米作为出口.设矩形的一边长为x米(如图),面积为y米2.
某杂技团用66米的幕布围成一个矩形临时场地,并留出2米作为出口.设矩形的一边长为x米(如图),面积为y米2.