题目内容
附加题:如图1,菱形纸片ABCD中,AB=1,∠B=60°,将纸片翻折(如图2),使D点落在AD所在直线上,并可在直线AD上运动,折痕为EF.当| 1 | 2 |
(1)线段AD与DG相等吗?△ADG与△BCG的面积之和是否随着DE的变化而变化?为什么?
(2)设AD=x,重叠部分(图3中阴影部分)的面积为y,求出y与x之间的函数关系式,并写出自变量x的取值范围以及面积y的取值范围.?

分析:(1)根据菱形性质,∠B=∠D=60°,又AD∥BC,不难得出△ADG为等边三角形,故AD=DG,可证△DAG、△BCG都为等边三角形,设AD=x,则有BC=1-x,用等边三角形计算面积的方法求解.
(2)平行四边形面积可以理解为S△ADG+S△BCG+2S阴影部分.
(2)平行四边形面积可以理解为S△ADG+S△BCG+2S阴影部分.
解答:解:(1)AD=DG.理由如下:
∵∠D=60°,∠DAB=∠B=60°
∴△DAG为等边三角形
∴AD=DG
△ADG与△BCG的面积和会随DE的变化而变化
设AD=x,则有BC=1-x
∵△DAG为等边三角形
∴△BCG也为等边三角形
∴S△ADG+S△BCG=
x2+
(1-x)2=
(2x2-2x+1)随x的变化而变化.
(2)∵2y=2×
×12-
x2-
(1-x)2
∴y=-
x2+
x+
(0<x<1,
<y≤
).
∵∠D=60°,∠DAB=∠B=60°
∴△DAG为等边三角形
∴AD=DG
△ADG与△BCG的面积和会随DE的变化而变化
设AD=x,则有BC=1-x
∵△DAG为等边三角形
∴△BCG也为等边三角形
∴S△ADG+S△BCG=
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
(2)∵2y=2×
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
∴y=-
| ||
| 4 |
| ||
| 4 |
| ||
| 8 |
| ||
| 8 |
3
| ||
| 16 |
点评:本题考查了菱形的性质,等边三角形的面积表示方法,用割补法表示阴影部分的面积等问题.

练习册系列答案
相关题目
 <DE<1时,设AB与DC相交于点G(如图).
<DE<1时,设AB与DC相交于点G(如图).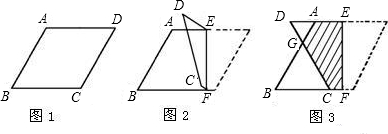
 <DE<1时,设AB与DC相交于点G(如图).
<DE<1时,设AB与DC相交于点G(如图).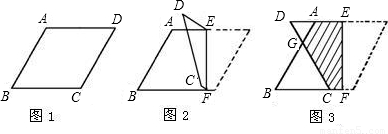
 <DE<1时,设AB与DC相交于点G(如图).
<DE<1时,设AB与DC相交于点G(如图).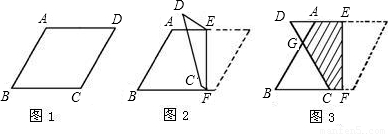
 <DE<1时,设AB与DC相交于点G(如图).
<DE<1时,设AB与DC相交于点G(如图).