题目内容
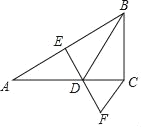
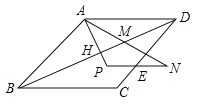
【题目】如图,E为菱形ABCD的边CD上任意点,将CE绕点E旋转一定角度后与AD平行.
(1)如图,若CE旋转后得到PE和NE,试判断下列结论是否成立?
①BD平分AN, ;
②BD⊥AP, (填写“成立”或“不成立”);
(2)证明(1)中你的判断.
(3)若∠ABC=60°,AB=BM=![]() +1,请直接写出CE的长度.
+1,请直接写出CE的长度.
【答案】(1)①成立;②成立;(2)见解析;(3)![]() .
.
【解析】
(1)根据题意、结合图形进行猜测;
(2)连接AC、PC、CN,根据等腰三角形的性质、三角形内角和定理证明∠ECP=∠DCA,得到A、P、C三点共线,根据菱形的性质证明即可;
(3)根据菱形的性质和余弦的定义求出BH,得到HM,根据三角形中位线定理求出CN,根据余弦的定义求出PN,根据直角三角形的性质解答即可.
(1)①BD平分AN,成立;
②BD⊥AP,成立.
故答案为:①成立;②成立;
(2)连接AC、PC、CN.
∵EP=EC,∴∠ECP=∠EPC,∴∠ECP=![]() =90°﹣
=90°﹣![]() ∠PEC,同理,∠DCA=90°﹣
∠PEC,同理,∠DCA=90°﹣![]() ∠ADC.
∠ADC.
∵PN∥AD,∴∠PEC=∠ADC,∴∠ECP=∠DCA,∴A、P、C三点共线.
∵四边形ABCD是菱形,∴BD⊥AC.
∵CE=PE=EN,∴∠PCN=90°,∴CN∥BD,又AH=HC,∴AM=MN,即BD平分AN;
(3)∵四边形ABCD是菱形,∴∠ABD=![]() ∠ABC=30°,∴BH=AB×cos30°=
∠ABC=30°,∴BH=AB×cos30°=![]() ,∴HM=BM﹣BH=
,∴HM=BM﹣BH=![]() +1﹣
+1﹣![]() =
=![]() .
.
∵∠ABC=60°,∴∠BAD=120°.
∵∠ABH=30°,∠AHB=90°,∴∠BAH=60°,∴∠DAC=120°-60°=60°.
∵AD∥PN,∴∠NPC=∠DAC=60°.
∵AH=HC,AM=MN,∴CN=2HM=![]() ﹣1,CN∥BD,∴∠PCN=∠BHC=90°,∴∠PNC=90°-60°=30°,∴PN=
﹣1,CN∥BD,∴∠PCN=∠BHC=90°,∴∠PNC=90°-60°=30°,∴PN=![]() =
=![]() ,∴CE=
,∴CE=![]() PN=
PN=![]() .
.

 名校课堂系列答案
名校课堂系列答案