Question

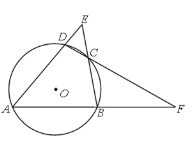
【题目】如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，

（1）求⊙O的半径；

（2）求O到弦BC的距离．

Answer 1

【答案】（1）5；（2）.

【解析】

（1）连结OB，设半径为r，则OE=r－2，运用垂径定理和勾股定理即可求解；

（2）利用S△BCO＝BCOF ＝OCBE即可求解.

（1）连结OB，设半径为r，则OE=r－2，

∵AC是⊙O的直径，弦BD⊥AO于E ，BD=8cm，

∴BE＝DE＝4 ，

在Rt△OBE中∵OE2+BE2=OB2 ，

∴(r－2)2＋42＝r2 ，

∴r=5；

（2）∵r＝5，

∴AC＝10，EC＝8

∴BC＝4；

∵OF⊥BC，

∴S△BCO＝BCOF ＝OCBE

∴4OF ＝5×4

∴OF＝ .