题目内容
 如图,每个小方格都是边长为1的正方形,
如图,每个小方格都是边长为1的正方形,(1)求四边形ABCD的面积;
(2)求角B的度数.
分析:(1)先求出正方形EFGH的面积,再分别求出四个小三角形的面积,进而可得出四边形ABCD的面积;
(2)先根据勾股定理求出AB、BC的长,再根据勾股定理的逆定理判断出△ABC的形状,进而可得出∠B的度数.
(2)先根据勾股定理求出AB、BC的长,再根据勾股定理的逆定理判断出△ABC的形状,进而可得出∠B的度数.
解答: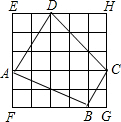 解:(1)∵每个小方格都是边长为1的正方形,
解:(1)∵每个小方格都是边长为1的正方形,
∴S□EFGH=5×5=25,
∴S四边形ABCD=S□EFGH-S△ADE-S△AFB-S△BCG-S△CDH
=25-
×2×3-
×2×4-
×1×2-
×3×3
=25-3-4-1-
=12.5;
(2)在Rt△ABF中,AB=
=
=2
,
在Rt△BGC中,BC=
=
=
,
∵(2
)2+(
)2=25=AC2,
∴△ABC是直角三角形,
∴∠B=90°.
 解:(1)∵每个小方格都是边长为1的正方形,
解:(1)∵每个小方格都是边长为1的正方形,∴S□EFGH=5×5=25,
∴S四边形ABCD=S□EFGH-S△ADE-S△AFB-S△BCG-S△CDH
=25-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=25-3-4-1-
| 9 |
| 2 |
=12.5;
(2)在Rt△ABF中,AB=
| AF2+BF2 |
| 22+42 |
| 5 |
在Rt△BGC中,BC=
| BG2+CG2 |
| 12+22 |
| 5 |
∵(2
| 5 |
| 5 |
∴△ABC是直角三角形,
∴∠B=90°.
点评:本题考查的是勾股定理的逆定理、勾股定理、三角形的面积公式及正方形的性质,涉及面较广,难度适中.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 24、如图,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.
24、如图,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系. ,得到对应△A′B′C′.
,得到对应△A′B′C′. 如图,每个小方格都是边长为1个单位长度的小正方形.
如图,每个小方格都是边长为1个单位长度的小正方形.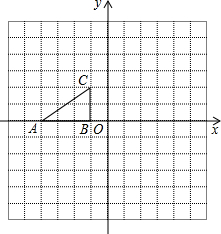 如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.
如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.