题目内容
 6、如图所示,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,下列结论错误的是( )
6、如图所示,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,下列结论错误的是( )分析:根据旋转的定义及性质,结合图形求解.
解答:解:∵将△ADC绕点A顺时针旋转90°后,得到△AFB,
∴点A是旋转中心,AF=AD,∠FAD=90°,△ADC≌△AFB,
故A、C、D正确,不符合题意;
B错误,符合题意.
故选B.
∴点A是旋转中心,AF=AD,∠FAD=90°,△ADC≌△AFB,
故A、C、D正确,不符合题意;
B错误,符合题意.
故选B.
点评:本题考查了旋转的定义及性质.
旋转的定义:在平面内,把一个图形绕某一定点O转动一个角度的图形变换叫做旋转,其中定点O叫做旋转中心,转动的角叫做旋转角.
旋转的性质:①对应点到旋转中心的距离相等.②对应点与旋转中心所连线段的夹角等于旋转角.③旋转前、后的图形全等.
旋转的定义:在平面内,把一个图形绕某一定点O转动一个角度的图形变换叫做旋转,其中定点O叫做旋转中心,转动的角叫做旋转角.
旋转的性质:①对应点到旋转中心的距离相等.②对应点与旋转中心所连线段的夹角等于旋转角.③旋转前、后的图形全等.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
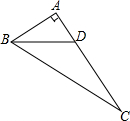 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( ) 21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB=
21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB=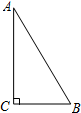 22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.
22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE. 如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB=
如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB= 如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.
如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.