题目内容
【题目】已知:Rt△ABC中,∠ACB=90°,AC=BC.
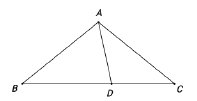
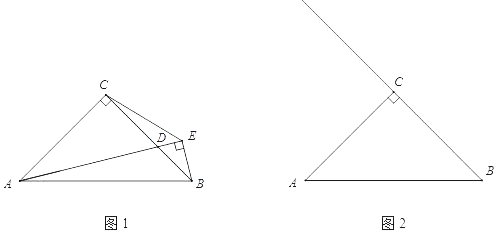
(1)如图1,点D是BC边上一点(不与点B,C重合),连接AD,过点B作BE⊥AD,交AD的延长线于点E,连接CE.若∠BAD=α,求∠DBE的大小(用含α的式子表示);
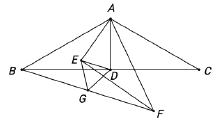
(2)如图2,点D在线段BC的延长线上时,连接AD,过点B作BE⊥AD,垂足E在线段AD上,连接CE.
①依题意补全图2;
②用等式表示线段EA,EB和EC之间的数量关系,并证明.
【答案】(1)∠DBE=![]() .;(2)①补全图形如图见解析;②猜想:当D在BC边的延长线上时,EB - EA =
.;(2)①补全图形如图见解析;②猜想:当D在BC边的延长线上时,EB - EA =![]() EC. 证明见解析.
EC. 证明见解析.
【解析】
(1)根据等腰直角三角形的性质得到∠CAB=45°,即可求出∠CAD=![]() .根据三角形的内角和即可求出∠DBE=∠CAD=
.根据三角形的内角和即可求出∠DBE=∠CAD=![]() .
.
(2)①根据题目要求作图即可.
②过点C作CF⊥CE,交AD的延长线于点F.根据三角形的内角和定理得到∠CAF =∠CBE,证明△ACF≌△BCE.根据全等三角形的性质有AF=BE,CF=CE.根据等腰直角三角形的性质有EF=![]() EC.则有 AF -EA =
EC.则有 AF -EA =![]() EC,即可求出线段EA,EB和EC之间的数量关系.
EC,即可求出线段EA,EB和EC之间的数量关系.
(1)解: 依题意,∠CAB=45°,
∵∠BAD=α,
∴∠CAD=![]() .
.
∵∠ACB=90°,BE⊥AD,∠ADC=∠BDE,
∴∠DBE=∠CAD=![]() .
.
(2)解:
①补全图形如图
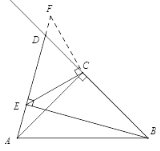
②猜想:当D在BC边的延长线上时,EB - EA =![]() EC.
EC.
证明:过点C作CF⊥CE,交AD的延长线于点F.

∵∠ACB=90°,
∴∠ACF=∠BCE.
∵CA=CB,∠CAF =∠CBE,
∴△ACF≌△BCE.
∴AF=BE,CF=CE.
∵∠ECF=90°,
∴EF=![]() EC.
EC.
即AF -EA =![]() EC.
EC.
∴EB -EA =![]() EC.
EC.

【题目】雾霾天气严重影响市民的生活质量。在今年寒假期间,某校九年级一班的综合实践小组学生对“雾霾天气的主要成因”随机调查了所在城市部分市民,并对调查结果进行了整理,绘制了下图所示的不完整的统计图表:
组别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 |
|
C | 炉烟气排放 | 15% |
D | 其他(滥砍滥伐等) |
|
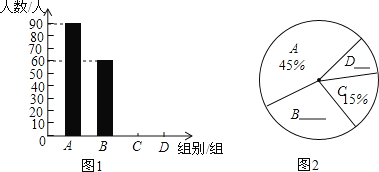
请根据统计图表回答下列问题:
(1)本次被调查的市民共有多少人?并求![]() 和
和![]() 的值;
的值;
(2)请补全条形统计图,并计算扇形统计图中扇形区域![]() 所对应的圆心角的度数;
所对应的圆心角的度数;
(3)若该市有100万人口,请估计市民认为“工业污染和汽车尾气排放是雾霾天气主要成因”的人数.