题目内容
先阅读第(1)题的解答过程,然后再解第(2)题.
(1)已知多项式2x3-x2+m有一个因式是2x+1,求m的值.
解法一:设2x3-x2+m=(2x+1)(x2+ax+b),
则:2x3-x2+m=2x3+(2a+1)x2+(a+2b)x+b
比较系数得
,解得
,∴m=
解法二:设2x3-x2+m=A•(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取x=-
,
2×(-
)3-(-
)2+m=0,故 m=
.
(2)已知x4+mx3+nx-16有因式(x-1)和(x-2),求m、n的值.
(1)已知多项式2x3-x2+m有一个因式是2x+1,求m的值.
解法一:设2x3-x2+m=(2x+1)(x2+ax+b),
则:2x3-x2+m=2x3+(2a+1)x2+(a+2b)x+b
比较系数得
|
|
| 1 |
| 2 |
解法二:设2x3-x2+m=A•(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取x=-
| 1 |
| 2 |
2×(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)已知x4+mx3+nx-16有因式(x-1)和(x-2),求m、n的值.
分析:设x4+mx3+nx-16=A(x-1)(x-2),对x进行两次赋值,可得出两个关于m、n的方程,联立求解可得出m、n的值.
解答:解:设x4+mx3+nx-16=A(x-1)(x-2)(A为整式),
取x=1,得1+m+n-16=0①,
取x=2,得16+8m+2n-16=0②,
由①、②解得m=-5,n=20.
取x=1,得1+m+n-16=0①,
取x=2,得16+8m+2n-16=0②,
由①、②解得m=-5,n=20.
点评:本题考查了因式分解的意义,阅读材料中提供了两种解题思路,同学们可以自己探索第二种解题方法.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
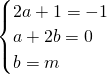 ,解得
,解得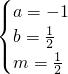 ,∴
,∴
 ,
,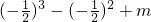 =0,故
=0,故 

 BC。
BC。 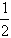 BC。
BC。 (AD+BC)吗?
(AD+BC)吗?