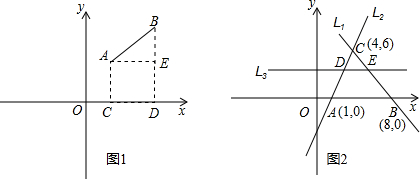题目内容
先阅读下面（1）题的解答过程，然后解答第（2）题
（1）已知，如图（1）所示，△ABC中，D、E分别是边AB、AC上的中点，连结DE。试说明DE与BC的关系。
解：DE与BC的关系为DE∥BC且DE=
BC。
理由如下：
将△ADE绕点D旋转180°到△BDF位置
根据旋转的特征，有F、D、E三点在同一直线上
∴DF=DE，BF=AE，且BF∥AE，
∴∠1=∠A，∠F=∠2
∵AE=EC
∴BF=EC
由于一组对边平行且相等的四边形为平行四边形
∴四边形FBCE是平行四边形
∴FE∥BC且FE=BC
即DE∥BC，DE=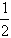
BC。
（2）已知：如图（2）所示，在梯形ABCD中，AD∥BC，E、F分别是AB、CD的中点，连结EF，试问你能根据（1）题的结论，说明EF∥BC，且EF=
（AD+BC）吗？
解：DE与BC的关系为DE∥BC且DE=
BC。 理由如下：
将△ADE绕点D旋转180°到△BDF位置
根据旋转的特征，有F、D、E三点在同一直线上
∴DF=DE，BF=AE，且BF∥AE，
∴∠1=∠A，∠F=∠2
∵AE=EC
∴BF=EC
由于一组对边平行且相等的四边形为平行四边形
∴四边形FBCE是平行四边形
∴FE∥BC且FE=BC
即DE∥BC，DE=
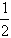BC。（2）已知：如图（2）所示，在梯形ABCD中，AD∥BC，E、F分别是AB、CD的中点，连结EF，试问你能根据（1）题的结论，说明EF∥BC，且EF=
（AD+BC）吗？解：连结AF，将△ADF绕点F旋转180°到△GCF位置。由旋转的特征得
AD∥CG，且AD=CG，A、F、G在一直线上，且AF=GF
∵AD∥BC，AD∥CG
∴B、C、G三点在一直线上
由于点E、F为△ABG的边AB、AG中点
∴EF∥BG，且EF=
BG
即EF∥BC，且EF=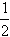
（AD+BC）。
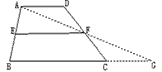
AD∥CG，且AD=CG，A、F、G在一直线上，且AF=GF
∵AD∥BC，AD∥CG
∴B、C、G三点在一直线上
由于点E、F为△ABG的边AB、AG中点
∴EF∥BG，且EF=
BG 即EF∥BC，且EF=
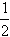（AD+BC）。
练习册系列答案
相关题目
先阅读下面的材料，再解答后面的各题：
现代社会对保密要求越来越高，密码正在成：为人们生活的一部分．有一种密码的明文（真实文）按计算机键盘字母排列分解，其中Q、W、E、…、N、M这26个字母依次对应1，2，3…25，26这26个自然数（见下表）：
给出一个变换公式：
将明文转换成密文，如：4?
+17=19，即R变为L．
11?
+8=12，即A变为S．
将密文转换成明文，如：21?3×（21-17）-2=10，即X变为P
13?3×（13-8）-1=14，即D变为F．
（1）按上述方法将明文NET译为密文；
（2）若按上述方法将明文译成的密文为DWN，请找出它的明文．
现代社会对保密要求越来越高，密码正在成：为人们生活的一部分．有一种密码的明文（真实文）按计算机键盘字母排列分解，其中Q、W、E、…、N、M这26个字母依次对应1，2，3…25，26这26个自然数（见下表）：
| Q | W | E | R | T | Y | U | I | O | P | A | S | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| F | G | H | J | K | L | Z | X | C | V | B | N | M |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|
将明文转换成密文，如：4?
| 4+2 |
| 3 |
11?
| 11+1 |
| 3 |
将密文转换成明文，如：21?3×（21-17）-2=10，即X变为P
13?3×（13-8）-1=14，即D变为F．
（1）按上述方法将明文NET译为密文；
（2）若按上述方法将明文译成的密文为DWN，请找出它的明文．