题目内容
先阅读下列第(1)题的解答过程,再解第(2)题.(1)已知实数a、b满足a2=2-2a,b2=2-2b,且a≠b,求
| a |
| b |
| b |
| a |
解:由已知得:a2+2a-2=0,b2+2b-2=0,且a≠b,故a、b是方程:x2+2x-2=0的两个不相等的实数根,由根与系数的关系得:a+b=-2,ab=-2.
∴
| a |
| b |
| b |
| a |
| (a+b)2-2ab |
| ab |
(2)已知p2-2p-5=0,5q2+2q-1=0,其中p、q为实数,求p2+
| 1 |
| q2 |
分析:根据一元二次方程根与系数的关系和通过代数式变形,转化为根与系数的关系解答则可.
解答:解:由5q2+2q-1=0两边同除以-q2,得:
-
-5=0,而p2-2p-5=0,
故p和
是方程x2-2x-5=0的两根,
由根与系数的关系得:p+
=2,p•
=-5,
所以p2+
=(p+
)2-2×
=14.
| 1 |
| q2 |
| 2 |
| q |
故p和
| 1 |
| q |
由根与系数的关系得:p+
| 1 |
| q |
| 1 |
| q |
所以p2+
| 1 |
| q2 |
| 1 |
| q |
| p |
| q |
点评:本题考查了一元二次方程根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
 ,β=-1-2
,β=-1-2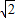 ,β=-1-2
,β=-1-2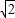 .
.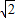 )2+3(-1-2
)2+3(-1-2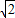 )2+4(-1-2
)2+4(-1-2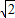 )
)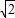 +3(9+4
+3(9+4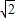 )-4-8
)-4-8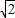 =32.
=32.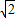 ,β=-1+2
,β=-1+2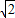 时,同理可得a2+3β2+4β=32.
时,同理可得a2+3β2+4β=32.