Question

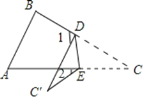
【题目】如图，∠BAC＝90°，AB＝AC，∠B =∠ACB=45°, AE⊥AD，且AE＝AD，若AB＝6cm，则四边形ADCE的面积为___．

Answer 1

【答案】18cm2．

【解析】

由“SAS”可证△ABD≌△ACE，可得四边形ADCE的面积=△ADC的面积+△ACE的面积=△ADC的面积+△ABD的面积=△ABC的面积，即可得出结论．

∵AE⊥AD，∴∠DAE=90°．

∵∠BAC=90°，∴∠BAD=∠CAE．

在△ABD和△ACE中，∵AB=AC，∠BAD=∠CAE，AD=AE，∴△ABD≌△ACE，∴四边形ADCE的面积=△ADC的面积+△ACE的面积=△ADC的面积+△ABD的面积=△ABC的面积=×AB×AC=×6×6=18（cm2）．

故答案为：18cm2．