题目内容
【题目】在边长为1的正方形ABCD中，点E是射线BC上一动点，AE与BD相交于点M，AE或其延长线与DC或其延长线相交于点F，G是EF的中点,连结CG．
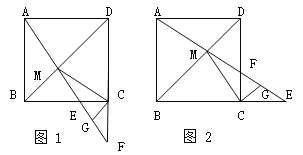
（1）如图1，当点E在BC边上时．求证：①△ABM≌△CBM；②CG⊥CM.
（2）如图2，当点E在BC的延长线上时,（1）中的结论②是否成立？请写出结论，不用证明．
（3）试问当点E运动到什么位置时，△MCE是等腰三角形?请说明理由.
【答案】（1）①证明见解析；②证明见解析；（2）成立；（3）当BE=
戓BE=
时，△MCE是等腰三角形.
【解析】试题（1）①根据正方形的性质，利用边角边定理即可证明△ABM≌△CBM；②根据全等三角形的性质可得∠BAM=∠BCM，根据“直角三角形斜边上的中线等于斜边的一半”可得GC=GF，根据等腰三角形和平行线的性质得到角的等量关系得∠BCM=∠GCF，即可证得结论；（2）类比（1）的方法即可得结论；（3）分当点E在BC边上时和当点E在BC的延长线上时两种情况讨论求解即可.
试题解析：
(1)①证明：∵四边形ABCD是正方形
∴AB=BC，∠ABM=∠CBM 又∵BM=BM,∴ΔABM≌ΔCBM.
②∵ΔABM≌ΔCBM，∴∠BAM=∠BCM 又∵∠ECF=90,G是EF的中点
∴GC=GF,∴∠GCF=∠F
又∵AB∥DF,∴∠BAM=∠F，∴∠BCM=∠GCF
∴∠BCM+∠GCE=∠GCF+∠GCE=90
∴GC⊥CM
(2)成立
(3)①当点E在BC边上时
∵∠MEC＞90,要使△MCE是等腰三角形,必须EM=EC,∴∠EMC=∠ECM
∴∠AEB=2∠BCM=2∠BAE，∴2∠BAE+∠BAE=90,∴∠BAE=300
∴BE=.
②当点E在BC的延长线上时,仿①易知BE=.
综上①②,当BE=戓BE=时，△MCE是等腰三角形.
