题目内容
已知二次函数y=mx2-7x-7的图象和x轴有交点,则m的取值范围是( )
A、m>-
| ||
B、m>-
| ||
C、m≥-
| ||
D、m≥-
|
分析:运用二次函数的性质及b2-4ac的取值特点解题.
解答:解:因为二次函数y=mx2-7x-7的图象和x轴有交点,所以b2-4ac=49+28m≥0;
所以m≥-
,又因为二次项系数m≠0;
所以m≥-
且m≠0.
故选D.
所以m≥-
| 7 |
| 4 |
所以m≥-
| 7 |
| 4 |
故选D.
点评:此题考查了二次函数的性质与x轴交点的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
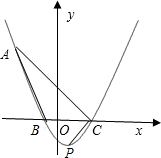 点C,顶点为P.
点C,顶点为P.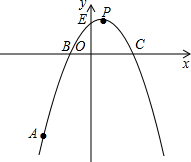 已知二次函数
已知二次函数