题目内容
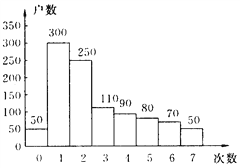
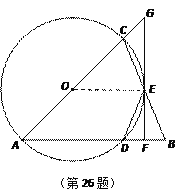
【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O与边AB、BC分别交于点D、E.过E的直线与⊙O相切,与AC的延长线交于点G,与AB交于点F.
(1)求证:△BDE为等腰三角形;
(2)求证:GF⊥AB;
(3)若⊙O半径为3,DF=1,求CG的长.
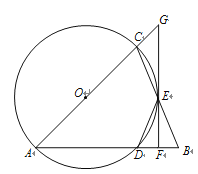
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】(1)∵四边形ACED是⊙O的内接四边形,
∴∠ACB+∠ADE=180°.………1分
 ∵∠BDE+∠ADE=180°,∴∠BDE=∠ACB.………2分
∵∠BDE+∠ADE=180°,∴∠BDE=∠ACB.………2分
∵AB=AC,∴∠B=∠ACB.
∴∠B=∠BDE,∴△BDE为等腰三角形.…………3分
(2)连结OE,∵直线FG与⊙O相切,
∴∠OEG=90°.…………4分
∵OC=OE,∴∠OEC=∠ACB.
∵∠B=∠ACB,∴∠B=∠OEC,∴OE∥AB.……5分
∴∠AFG=∠OEG=90°,即GF⊥AB. …………6分
(3)设CG=x.∵△BDE为等腰三角形,GF⊥AB,
∴BF=DF=1,AF=AB-BF=AC-BF=5.………………7分
∵OE∥AB,∴△GOE∽△GAF,∴![]() =
=![]() , …………8分
, …………8分
∴![]() =
=![]() ,解得x=
,解得x=![]() ,即CG=
,即CG=![]() .
.

练习册系列答案
相关题目