题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,以
,以![]() 为直角边在
为直角边在![]() 左侧作等腰三角形
左侧作等腰三角形![]() ,其中
,其中![]() ,连接
,连接![]() .
.
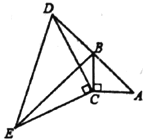
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
(3)![]() 与
与![]() 有何位置关系?请说明理由.
有何位置关系?请说明理由.
【答案】(1)见解析;(2)6cm;(3)![]() ,见解析.
,见解析.
【解析】
(1)根据等腰直角三角形的性质得到CD=CE,CA=CB,然后利用“SAS”可判断△ACD≌△BCE;
(2)根据全等三角形的性质得到AD=BE,而DB=AB=3cm,所以BE=6cm;
(3)根据全等三角形的性质得到∠1=∠2,而∠3=∠4,然后根据三角形内角和定理即可得到∠EBD=∠ECD=90°
(1)证明:∵![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
∵![]() .
.
∴![]() ;
;
(2)解:∵![]() ,
,![]()
∴![]() ,
,
∵![]() ;
;
∴![]() ,
,
即BE的长为![]() .
.
(3)![]() .
.
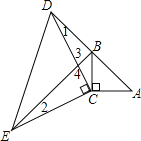
理由如下:
如图:
∵△ACD≌△BCE,
∴∠1=∠2,
而∠3=∠4,
∴∠EBD=∠ECD=90°,
∴BE⊥AD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
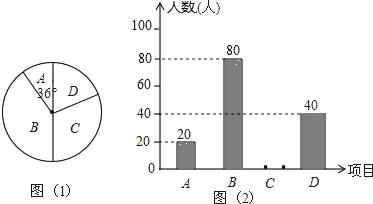
【题目】某中学为了了解学生对手机的依赖程度,开展了一次“学生周末手机使用时间”抽样调查,根据调查结果绘制了如下两种不完整的统计图表.
组别 | 周末手机使用时间 | 人数 |
|
| 20 |
|
|
|
|
| 22 |
|
| 10 |
|
| 8 |
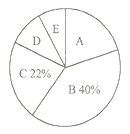
请根据图表信息解答下列问题:
(1)本次抽样,共调查了 人;
(2)扇形统计图中“![]() ”所对应的圆心角的度数是/span> ;
”所对应的圆心角的度数是/span> ;
(3)估计该校2450名学生中周末手机使用时间小于2小时的人数.