题目内容
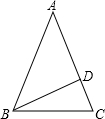
已知：如图，△ABC中，AB=AC，D为AC上一点，∠DBC=
∠A．
求证：AC⊥BD．
| 1 |
| 2 |
求证：AC⊥BD．
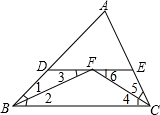
证明：过点A作AE⊥BC交BC于E，交BD于F…（1分）
∵AB=AC，AE⊥BC，
∴∠CAE=
∠BAC．
∵∠DBC=
∠BAC，
∴∠CAE=∠DBC…（3分）
∵∠1=∠2，
∴∠ADF=180°-∠2-∠CAE∠BEF=180°-∠1-∠DBC．
∴∠ADF=∠BEF=90°…（5分）
∴BD⊥AC．…（6分）
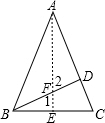
∵AB=AC，AE⊥BC，
∴∠CAE=
| 1 |
| 2 |
∵∠DBC=
| 1 |
| 2 |
∴∠CAE=∠DBC…（3分）
∵∠1=∠2，
∴∠ADF=180°-∠2-∠CAE∠BEF=180°-∠1-∠DBC．
∴∠ADF=∠BEF=90°…（5分）
∴BD⊥AC．…（6分）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
