题目内容
【题目】如图,AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30°,∠APB=60°.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,求弦AB及PA,PB的长.
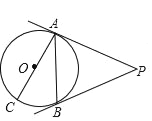
【答案】(1)见解析;(2)2
【解析】
试题(1)连接OB,证PB⊥OB.根据四边形的内角和为360°,结合已知条件可得∠OBP=90°得证;
(2)连接OP,根据切线长定理得直角三角形,根据含30度角的直角三角形的性质即可求得结果。
(1)连接OB.
∵OA=OB,∴∠OBA=∠BAC=30°.
∴∠AOB=80°-30°-30°=20°.
∵PA切⊙O于点A,∴OA⊥PA,
∴∠OAP=90°.
∵四边形的内角和为360°,
∴∠OBP=360°-90°-60°-20°=90°.
∴OB⊥PB.
又∵点B是⊙O上的一点,
∴PB是⊙O的切线.
(2)连接OP,
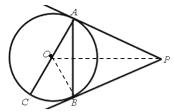
∵PA、PB是⊙O的切线,
∴PA=PB,∠OPA=∠OPB=![]() ,∠APB=30°.
,∠APB=30°.
在Rt△OAP中,∠OAP=90°,∠OPA=30°,
∴OP=2OA=2×2=4.
∴PA=OP2-OA2=2
∵PA=PB,∠APB=60°,
∴PA=PB=AB=2。

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目