Question

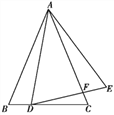
【题目】如图，在△ABC中，∠ABC＝80°，∠BAC＝40°，AB的垂直平分线分别与AC、AB交于点D、E．

（1）在图中作出AB的垂直平分线DE，并连接BD．

（2）证明：△ABC∽△BDC．

Answer 1

【答案】（1）见解析（2）证明见解析

【解析】

（1）分别以A、B为圆心，大于AB的长为半径画弧，两弧交于两点，过两点作直线，即为AB的垂直平分线；

（2）由线段垂直平分线的性质，得DA=DB，则∠ABD=∠BAC=40°，从而求得∠CBD=40°，即可证出△ABC∽△BDC．

（1）如图，DE即为所求；

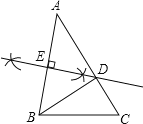
（2）∵DE是AB的垂直平分线，

∴BD＝AD，

∴∠ABD＝∠A＝40°，

∴∠DBC＝∠ABC﹣∠ABD＝80°﹣40°＝40°，

∴∠DBC＝∠BAC，

∵∠C＝∠C，

∴△ABC∽△BDC．