题目内容
【题目】如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米.
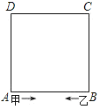
(1)出发后 分钟时,甲乙两人第一次在正方形的顶点处相遇;
(2)如果用记号(a,b)表示两人行了a分钟,并相遇过b次,那么当两人出发后第一次处在正方形的两个相对顶点位置时,对应的记号应是 .
【答案】(1)2;(2)(6,13).
【解析】
试题分析::(1)∵两个人的速度之和是85米每分钟,![]() 分钟后两人第一次相遇.如果要两人在顶点相遇,则:每个人所走的路程均为10的整数倍,且两个人所走路程之和为10+40n(n是指边得条数).S=10+40n,n为0、1、2、3…n ①,S甲=55t可以被10整除t为2、4、6…②,S乙=30t也可以被10整除t为甲方取值即可,∵S=S甲+S乙,整理得:55t+30t=10+40n,即:85t=10+40n,∴n=
分钟后两人第一次相遇.如果要两人在顶点相遇,则:每个人所走的路程均为10的整数倍,且两个人所走路程之和为10+40n(n是指边得条数).S=10+40n,n为0、1、2、3…n ①,S甲=55t可以被10整除t为2、4、6…②,S乙=30t也可以被10整除t为甲方取值即可,∵S=S甲+S乙,整理得:55t+30t=10+40n,即:85t=10+40n,∴n=![]() ③,由①②③得:当t=2时,两人第一次在顶点相遇.此时甲走了110米,乙走了60米,相遇在点D.(2)点甲、乙相遇则两者走时间相同,设甲走x米,则乙走
③,由①②③得:当t=2时,两人第一次在顶点相遇.此时甲走了110米,乙走了60米,相遇在点D.(2)点甲、乙相遇则两者走时间相同,设甲走x米,则乙走![]() x=
x=![]() x米,∵要相遇在正方形顶点,∴x和
x米,∵要相遇在正方形顶点,∴x和![]() x都要为10的整数倍且x+
x都要为10的整数倍且x+![]() x-10=
x-10=![]() x-10为40的整数倍(除第一次走10米相遇,以后每次相遇都要再走40米),∴(a-
x-10为40的整数倍(除第一次走10米相遇,以后每次相遇都要再走40米),∴(a-![]() )×85=40(b-1)+20,由(1)可知:当a=6时,甲走了330米,甲走到点B,乙走了180米,走到点D,解得:b=13,故答案为:(6,13)
)×85=40(b-1)+20,由(1)可知:当a=6时,甲走了330米,甲走到点B,乙走了180米,走到点D,解得:b=13,故答案为:(6,13)

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目