题目内容
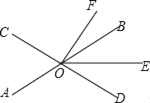
【题目】如图1，已知△ABC中，AB＝BC＝1，∠ABC＝90°，把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上（直角三角板的短直角边为DE，长直角边为DF），将直角三角板DEF绕D点按逆时针方向旋转．
（1）在图1中，DE交AB于M，DF交BC于N．
①求证:DM＝DN；
②在这一旋转过程中，直角三角板DEF与△ABC的重叠部分为四边形DMBN，请说明四边形DMBN的面积是否发生变化？若发生变化，请说明是如何变化的？若不发生变化，求出其面积；
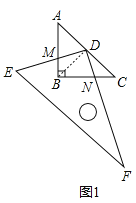
（2）继续旋转至如图2的位置，延长AB交DE于M，延长BC交DF于N，DM＝DN是否仍然成立？若成立，请给出证明；若不成立，请说明理由；
（3）继续旋转至如图3的位置，延长FD交BC于N，延长ED交AB于M，DM＝DN是否仍然成立？请写出结论，不用证明．
【答案】（1）①证明详见解析；②四边形DMBN的面积不发生变化，理由详见解析；
（2）DM=DN仍然成立，理由详见解析；（3）DM=DN．
【解析】
试题分析：（1）①连接DB，根据AAS证明△BMD≌△CND，所以DM=DN；
②由①知△BMD≌△CND，所以
，所以四边形DMBN的面积等于△ABC的面积的一半；
（2）连接DB，依然可以证得△BMD≌△CND，所以DM=DN；
（3）根据（2）的思路可以得到DM=DN．
试题解析：（1）①证明：连接DB，
在Rt△ABC中，因为AB=BC，AD=DC，所以DB=DC=AD，∠BDC=90°，
所以∠ABD=∠C=45°，
因为∠MDB+∠BDN=∠CDN+∠BDN=90°，
所以∠MDB=∠NDC，
所以△BMD≌△CND，所以DM=DN．
②四边形DMBN的面积不发生变化，理由如下：
由①知△BMD≌△CND，所以，所以
=
=
．
（2）DM=DN仍然成立，理由如下：
连接DB，在Rt△ABC中，因为AB=BC，AD=DC，所以DB=DC=AD，∠BDC=90°，所以∠DCB=∠DBC=45°，所以∠DBM=∠DCN=135°，因为∠NDC+∠CDM=∠BDM+∠CDM=90°，所以∠MDB=∠NDC，所以△BMD≌△CND，所以DM=DN．
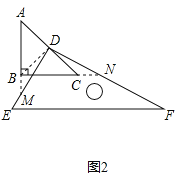
（3） DM=DN．
