题目内容
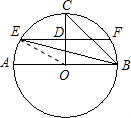
如图,⊙O中,半径CO垂直于直径AB,D为OC的中点,过D作弦EF∥AB,则∠CBE=______.


连接OE,如图,
∵半径CO垂直于直径AB,而EF∥AB,
∴∠EDO=90°,
又∵D为OC的中点,
∴OD=
OC=
OE,
∴∠OED=30°,
∴∠EOD=60°,
∴∠CBE=
∠EOD=
×60°=30°.
故答案为:30°.
∵半径CO垂直于直径AB,而EF∥AB,
∴∠EDO=90°,
又∵D为OC的中点,
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OED=30°,
∴∠EOD=60°,
∴∠CBE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:30°.


练习册系列答案
相关题目





