题目内容
【题目】如图,直线AB:y=﹣![]() x+
x+![]() 交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.
交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.
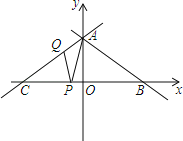
(1)点B的坐标是( , );∠ABC= 度;
(2)若⊙O与AB相切,则⊙O的半径等于 ;
(3)当P点坐标为(﹣2,0)时,求CQ的长;
(4)当△APQ为等腰三角形时,求P点的坐标.
【答案】(1)(8,0);30;(2)4;(3)CQ的长为![]() ;(4)当△APQ为等腰三角形时,P点的坐标为(8,0)或(﹣
;(4)当△APQ为等腰三角形时,P点的坐标为(8,0)或(﹣![]() ,0)或(
,0)或(![]() ﹣8,0).
﹣8,0).
【解析】
试题分析:(1)由B点是直线AB与x轴的交点,故令y=0,解出x的值即为B点的坐标,A点是直线AB与y轴的交点,令x=0,可得出A点坐标,由三角函数的正弦值可得出∠ABC的值;(2)圆与直线相切,圆的半径就等于圆心到直线的距离,结合点到直线的距离公式即可得出结论;(3)由两个等于30°的角和一个公共角可得出△CAP∽△PAQ,根据相似三角形的性质可找出AQ的值,再由CQ=AC﹣AQ,即可得出结论;(4)若三角形为等腰三角形,只需两条边相等即可,在此分哪两条边相等来讨论,即可得出结论.
解:(1)令y=0,则有0=﹣![]() x+
x+![]() ,
,
解得:x=8.
即点B的坐标是(8,0).
令x=0,则有y=![]() ,
,
即点A的坐标为(0,![]() ).
).
∴AO=![]() ,BO=8,
,BO=8,
∴tan∠ABO=![]() =
=![]() ,
,
∴∠ABO=30°.
故答案为:(8,0);30.
(2)∵⊙O与AB相切,
∴⊙O的半径为点O到直线AB的距离.
直线AB:y=﹣![]() x+
x+![]() 可变形为
可变形为![]() x+y﹣
x+y﹣![]() =0.
=0.
点O到直线AB的距离=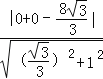 =4.
=4.
∴⊙O的半径为4.
故答案为:4.
(3)∵直线AC与AB关于y轴对称,
∴点C坐标为(﹣8,0),∠ACB=∠ABC=30°.
又∵点A的坐标为(0,![]() ),点P的坐标为(﹣2,0),
),点P的坐标为(﹣2,0),
∴AO=![]() ,CO=8,AC=
,CO=8,AC=![]() =
=![]() ,PO=2,CP=CO﹣PO=6,AP=
,PO=2,CP=CO﹣PO=6,AP=![]() =
=![]() .
.
∵∠CAP=∠PAQ,∠ACP=∠APQ=30°,
∴△CAP∽△PAQ,
∴![]() =
=![]() ,AQ=
,AQ=![]() =
=![]() .
.
CQ=AC﹣AQ=![]() .
.
故当P点坐标为(﹣2,0)时,CQ的长为![]() .
.
(4)△APQ为等腰三角形分三种情况:
①当AQ=PQ时,如图1,
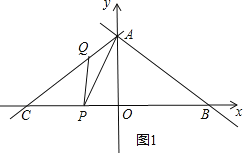
∵∠APQ=30°,AQ=PQ,
∴∠PAQ=30°,
∵∠ACO=30°,∠CAO=90°﹣∠ACO=60°,
∴∠PAO=∠CAO﹣∠PAQ=30°.
∵AO⊥BC,
∴PO=AOtan∠PAO=![]() ,
,
∴点P的坐标为(﹣![]() ,0).
,0).
②当AP=AQ时,如图2,
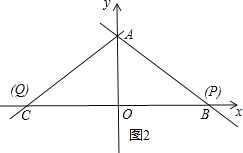
此时P点与B点重合,Q点与C点重合,
∴点P的坐标为(8,0).
③当AP=PQ时,如图3,
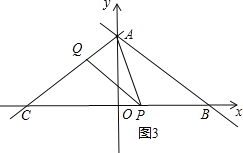
∵∠APQ=30°,∠PAQ=∠PQA=![]() =75°,
=75°,
∴∠CPA=180°﹣∠ACP﹣CAP=180°﹣30°﹣75°=75°,
∴∠CAP=∠CPA=75°,
∴CP=CA=![]() ,
,
OP=CP﹣CO=![]() ﹣8.
﹣8.
∴点P的坐标为(![]() ﹣8,0).
﹣8,0).
综上可知:当△APQ为等腰三角形时,P点的坐标为(8,0)或(﹣![]() ,0)或(
,0)或(![]() ﹣8,0).
﹣8,0).

 优学名师名题系列答案
优学名师名题系列答案【题目】父亲告诉小明:“距离地面越高,温度越低”,并且出示了下面的表格:
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃) | 20 | 14 | 8 | 2 | ﹣4 | ﹣10 |
那么根据表格中的规律,距离地面6千米的高空温度是( )
A. ﹣10℃ B. ﹣16℃ C. ﹣18℃
D. ﹣20℃
