题目内容
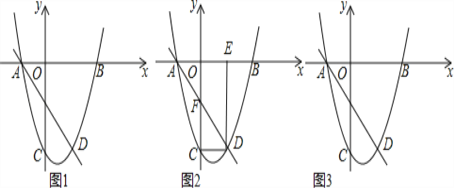
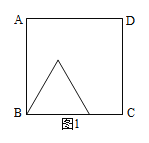
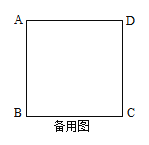
【题目】如图1,图2中,正方形ABCD的边长为6,点P从点B出发沿边BC—CD以每秒2个单位长的速度向点D匀速运动,以BP为边作等边三角形BPQ,使点Q在正方形ABCD内或边上,当点Q恰好运动到AD边上时,点P停止运动。设运动时间为t秒(t≥0)。
(1)当t=2时,点Q到BC的距离=_____;
(2)当点P在BC边上运动时,求CQ的最小值及此时t的值;
(3)若点Q在AD边上时,如图2,求出t的值;
(4)直接写出点Q运动路线的长。

【答案】(1)![]() ;(2)t=
;(2)t=![]() ,CQ=3
,CQ=3![]() ;(3)
;(3) ![]() ;(4)
;(4) ![]()
【解析】试题分析:![]() 过点
过点![]() 作
作![]() 用三角函数的知识即可求出点Q到BC的距离,
用三角函数的知识即可求出点Q到BC的距离,
![]() 点P在BC边上运动时,有
点P在BC边上运动时,有![]() ,根据垂线段最短,当
,根据垂线段最短,当![]() 时,CQ最小,作图,求解即可.
时,CQ最小,作图,求解即可.
![]() 若点Q在AD边上,则
若点Q在AD边上,则![]() 证明Rt△BAQ≌Rt△BCP,
证明Rt△BAQ≌Rt△BCP,![]()
根据![]() 列出方程求解即可.
列出方程求解即可.
![]() 点Q运动路线的长等于点
点Q运动路线的长等于点![]() 运动的路线长:
运动的路线长:![]()
试题解析:![]() 如图:
如图:
过点![]() 作
作![]()

当![]() 时,
时,![]()
![]() 是等边三角形,
是等边三角形,
![]()
![]()
故答案为:![]()
![]() 点P在BC边上运动时,有
点P在BC边上运动时,有![]() ,根据垂线段最短,当
,根据垂线段最短,当![]() 时,CQ最小,
时,CQ最小,
如图,在直角三角形BCQ中,![]() ,
,

![]()
![]()
∴![]()
∴![]()
∴![]()
(3)若点Q在AD边上,则![]()
∵![]()
∴Rt△BAQ≌Rt△BCP(HL),
∴![]()
∴![]()
∵![]() ,且由勾股定理可得,
,且由勾股定理可得,![]()
∴![]()
解得:![]() (不合题意,舍去),
(不合题意,舍去),![]()
∴![]() .
.
(4)点Q运动路线的长等于点![]() 运动的路线长:
运动的路线长:![]()


【题目】某运输部门规定:办理托运,当一件物品的重量不超过![]() 千克时,需付基础费
千克时,需付基础费![]() 元和保险费
元和保险费![]() 元;为了限制过重物品的托运,当一件物品的重量超过
元;为了限制过重物品的托运,当一件物品的重量超过![]() 千克时,除了付以上基础费和保险费外,超过部分每千克还需付
千克时,除了付以上基础费和保险费外,超过部分每千克还需付![]() 元的超重费.设某件物品的重量为
元的超重费.设某件物品的重量为![]() 千克,支付费用为
千克,支付费用为![]() 元.
元.
(1)当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
当![]() 时,
时,![]() ______________(用式子表示);
______________(用式子表示);
(2)甲、乙、丙三人各托运一件物品,物品的重量与支付费用如下表所示:
托运人 | 物品重量/千克 | 支付费用/元 |
甲 | 14 | 33 |
乙 | 20 | 39 |
丙 | 30 |
|
根据以上提供的信息确定![]() 的值,并计算出丙所支付的费用
的值,并计算出丙所支付的费用![]() .
.