题目内容
【题目】如图,已知点A、B分别是反比例函数y= ![]() (x>0),y=
(x>0),y= ![]() (x<0)的图象上的点,且,∠AOB=90°,则
(x<0)的图象上的点,且,∠AOB=90°,则 ![]() 的值为( )
的值为( ) 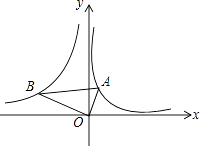
A.4
B.![]()
C.2
D.![]()
【答案】C
【解析】解:过点A作AE⊥x轴于点A,过点B作BF⊥x轴于点B,如图所示. 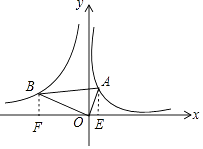
∵∠FOB+∠AOB+∠AOE=180°,∠AOB=90°,∠FOB+∠OBF=90°,
∴∠AOE=∠OBF.
又∵∠AEO=∠OFB=90°,
∴△AOE∽△OBF,
∴ ![]() =
= ![]() =
= ![]() =4,
=4,
∴ ![]() 的值为2.
的值为2.
故选C.
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】一辆汽车在公路上匀速行驶,下表记录的是汽车在加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时) | 0 | 1 | 2 | 2.5 |
余油量y(升) | 100 | 80 | 60 | 50 |
(1)小明分析上表中所给的数据发现x,y成一次函数关系,试求出它们之间的函数表达式(不要求写出自变量的取值范围);
(2)求汽车行驶4.2小时后,油箱内余油多少升?