题目内容
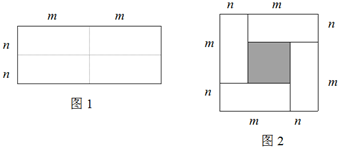
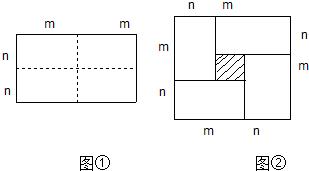
图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
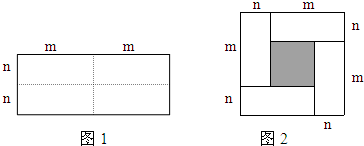
(1)你认为图2中的阴影部分的正方形的边长等于
(2)请用两种不同的方法求图2中阴影部分的面积.
①
②
(3)观察图2你能写出下列三个代数式之间的等量关系吗?
(m+n)2,(m-n)2,mn
(4)运用你所得到的公式,计算若mn=-2,m-n=4,求(m+n)2的值.
(5)用完全平方公式和非负数的性质求代数式x2+2x+y2-4y+7的最小值.

(1)你认为图2中的阴影部分的正方形的边长等于
m-n
m-n
?(2)请用两种不同的方法求图2中阴影部分的面积.
①
(m-n)2
(m-n)2
;②
(m+n)2-4mn
(m+n)2-4mn
.(3)观察图2你能写出下列三个代数式之间的等量关系吗?
(m+n)2,(m-n)2,mn
(m-n)2=(m+n)2-4mn
(m-n)2=(m+n)2-4mn
.(4)运用你所得到的公式,计算若mn=-2,m-n=4,求(m+n)2的值.
(5)用完全平方公式和非负数的性质求代数式x2+2x+y2-4y+7的最小值.
分析:(1)根据阴影部分正方形的边长等于小长方形的长减去宽解答;
(2)从整体与局部两个思路考虑解答;
(3)根据大正方形的面积减去阴影部分小正方形的面积等于四个长方形的面积解答;
(4)把数据代入(3)的数量关系计算即可得解;
(5)根据完全平方公式配方,再根据非负数的性质即可得解.
(2)从整体与局部两个思路考虑解答;
(3)根据大正方形的面积减去阴影部分小正方形的面积等于四个长方形的面积解答;
(4)把数据代入(3)的数量关系计算即可得解;
(5)根据完全平方公式配方,再根据非负数的性质即可得解.
解答:解:(1)由图可知,阴影部分小正方形的边长为:m-n;
(2)根据正方形的面积公式,阴影部分的面积为(m-n)2,
还可以表示为(m+n)2-4mn;
(3)根据阴影部分的面积相等,(m-n)2=(m+n)2-4mn;
(4)∵mn=-2,m-n=4,
∴(m+n)2=(m-n)2+4mn=42+4×(-2)=16-8=8;
(5)x2+2x+y2-4y+7,
=x2+2x+1+y2-4y+4+2,
=(x+1)2+(y-2)2+2,
∵(x+1)2≥0,(y-2)2≥0,
∴(x+1)2+(y-2)2≥2,
∴当x=-1,y=2时,代数式x2+2x+y2-4y+7的最小值是2.
故答案为:(1)m-n;(2)(m-n)2,(m+n)2-4mn;(3)(m-n)2=(m+n)2-4mn.
(2)根据正方形的面积公式,阴影部分的面积为(m-n)2,
还可以表示为(m+n)2-4mn;
(3)根据阴影部分的面积相等,(m-n)2=(m+n)2-4mn;
(4)∵mn=-2,m-n=4,
∴(m+n)2=(m-n)2+4mn=42+4×(-2)=16-8=8;
(5)x2+2x+y2-4y+7,
=x2+2x+1+y2-4y+4+2,
=(x+1)2+(y-2)2+2,
∵(x+1)2≥0,(y-2)2≥0,
∴(x+1)2+(y-2)2≥2,
∴当x=-1,y=2时,代数式x2+2x+y2-4y+7的最小值是2.
故答案为:(1)m-n;(2)(m-n)2,(m+n)2-4mn;(3)(m-n)2=(m+n)2-4mn.
点评:本题考查了完全平方公式的几何背景,准确识图,根据阴影部分的面积的两种不同表示方法得到的代数式的值相等列式是解题的关键.

练习册系列答案
相关题目
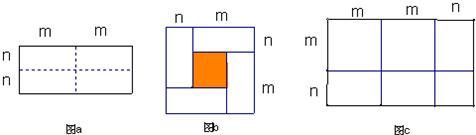
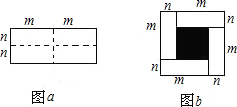 如图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均匀分成四块形状大小完全一样的小长方形,然后按图b形状拼成一个大正方形.
如图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均匀分成四块形状大小完全一样的小长方形,然后按图b形状拼成一个大正方形.