Question

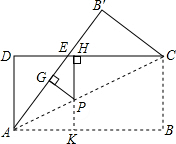
如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E．
（1）试找出一个与△AED全等的三角形，并加以证明．
（2）若AB=8，DE=3，P为线段AC上的任意一点，PG⊥AE于G，PH⊥EC于H，PG+PH的值会变化吗？若变化，请说明理由；若不变化，请求出这个值．

Answer 1

（1）△CEB′≌△AED；
证明：∵四边形ABCD是矩形，
∴AB∥CD，
∴∠ECA=∠CAB，∠D=∠B=90°，
由折叠的性质得：∠EAC=∠CAB，∠B′=∠B，
∴∠EAC=∠ECA，∠B′=∠D，
∴EA=EC，
在△AED和△CEB′中，
∵

∠D=∠B′ ∠DEA=∠B′EC EA=EC

，
∴△CEB′≌△AED（AAS）；

（2）PG+PH的值不变．
∵△CEB′≌△AED，
∴EB′=DE=3，
∵AB′=AB=8，
∴AE=AB′-EB′=8-3=5，
在Rt△ADE中，AD=

AE2-DE2

=4，
过点P作PK⊥AB于K，
∵∠B′AC=∠BAC，PG⊥AE，
∴PG=PK，
∵PH⊥CD，AB∥CD，
∴PH⊥AB，
∴H，P，K共线，
∵∠D=∠KHD=∠HKA=90°，
∴四边形ADHK是矩形，
∴HK=AD=4，
∴PG+PH=PK+PH=HK=4．