Question

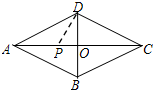
如图，在菱形纸片ABCD中，两对角线AC，BD长分别为16，12，折叠纸片使DO边落在边DA上，则折痕DP的长为（　　）

A．3 5

B． 5

C．3 3

D．3 2

Answer 1

设O点的对应点为E，连接PE，
由折叠的性质可得：PE=OP，DE=OD，
∵四边形ABCD是菱形，
∴AC⊥BD，OA=

1

2

AC=

1

2

×16=8，OB=

1

2

BD=

1

2

×12=6，
∴AD=

OA2+OD2

=10，
设OP=x，则PE=x，AE=AD-DE=10-6=4，AP=OA-OP=8-x，
在Rt△APE中，AP²=AE²+PE²，
即（8-x）²=4²+x²，
解得：x=3，
即OP=3，
∴DP=

OP2+OD2

=3

5

．
故选A．