题目内容
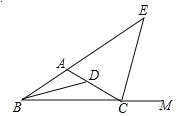
【题目】如图，在梯形ABCD中，AD∥BC，延长CB到点E，使BE=AD，连接DE交AB于点M．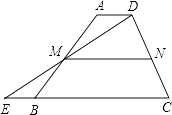 
（1）求证：△AMD≌△BME；
（2）若N是CD的中点，且MN=5，BE=2，求BC的长．
【答案】
（1）证明：∵AD∥BC，
∴∠A=∠MBE，∠ADM=∠E，
在△AMD和△BME中，
，
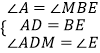∴△AMD≌△BME（ASA）
（2）解：∵△AMD≌△BME，
∴MD=ME，ND=NC，
∴MN= 
EC，
∴EC=2MN=2×5=10，
∴BC=EC﹣EB=10﹣2=8．
答：BC的长是8
【解析】（1）找出全等的条件：BE=AD，∠A=∠ABE，∠E=∠ADE，即可证明；（2）首先证得MN是三角形的中位线，根据MN= （BE+BC），又BE=2，即可求得．
【考点精析】掌握梯形的定义是解答本题的根本，需要知道一组对边平行，另一组对边不平行的四边形是梯形．两腰相等的梯形是等腰梯形．
练习册系列答案
同步练习强化拓展系列答案
相关题目
