题目内容
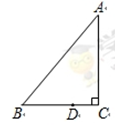
某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶,每级小台阶都为0.4米.现要做一个不锈钢的扶手AB及两根与FG垂直且长均为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且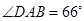 .
.

(1)求点D与点C的高度差DH的长度;
(2)求所用不锈钢材料的总长度.(结果精确到0.1米)
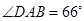 .
.
(1)求点D与点C的高度差DH的长度;
(2)求所用不锈钢材料的总长度.(结果精确到0.1米)
(1)1.2米.(2)4.9米.
试题分析:(1)通过图观察可知DH高度包含3层台阶,因而DH=每级小台阶高度×小台阶层数.
(2)首先过点B作BM⊥AH,垂足为M.求得AM的长,在Rt△AMB中,
根据余弦函数cosA=
 即可求得AB的长,那么根据不锈钢材料的总长度l=AD+AB+BC,求得所用不锈钢材料的长.
即可求得AB的长,那么根据不锈钢材料的总长度l=AD+AB+BC,求得所用不锈钢材料的长.(1)DH=0.4×3=1.2(米).
(2)过点B作BM⊥AH,垂足为M.(1分)
由题意得:MH=BC=AD=1,∠A=66°.
∴AM=AH-MH=1+1.2-1=1.2.(2分)
在Rt△AMB中,
∵cosA=

∴AB=
 (米).
(米).∴l=AD+AB+BC≈1+2.92+1≈4.9(米).
答:点D与点C的高度差DH为1.2米;所用不锈钢材料的总长度约为4.9米.
考点: 解直角三角形的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
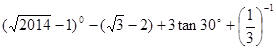

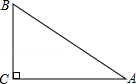

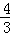


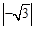 -(-4)-1+
-(-4)-1+ -2cos30°
-2cos30°
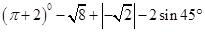
 ,即用a、b、
,即用a、b、