题目内容
智能手机如果安装了一款测量软件“Smart Measure”后,就可以测量物高、宽度和面积等.如图,打开软件后将手机摄像头的屏幕准星对准脚部按键,再对准头部按键,即可测量出人体的高度.其数学原理如图②所示,测量者AB与被测量者CD都垂直于地面BC.
(1)若手机显示AC=1m,AD=1.8m,∠CAD=60°,求此时CD的高.(结果保留根号)
(2)对于一般情况,试探索手机设定的测量高度的公式:设AC=a,AD=b,∠CAD= ,即用a、b、
,即用a、b、 来表示CD.(提示:sin2
来表示CD.(提示:sin2 +cos2
+cos2 =1)
=1)
(1)若手机显示AC=1m,AD=1.8m,∠CAD=60°,求此时CD的高.(结果保留根号)
(2)对于一般情况,试探索手机设定的测量高度的公式:设AC=a,AD=b,∠CAD=
 ,即用a、b、
,即用a、b、 来表示CD.(提示:sin2
来表示CD.(提示:sin2 +cos2
+cos2 =1)
=1)
(1)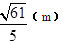 (2)
(2)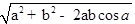
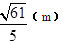 (2)
(2)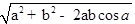
解:(1)作CH⊥AD于点H.

在Rt△ACH中,∵AC=1,∠CAH=60°,
∴AH= ,CH=
,CH=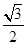 .
.
∵AD=1.8,
∴HD=1.3.
∴CD=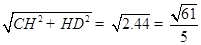 (m);
(m);
(2)同上可得,AH=acos ,CH=asin
,CH=asin .
.
∵AD=b,
∴HD=b﹣acos .
.
∴CD= .
.
考查了解直角三角形的应用,本题关键是熟悉三角函数、勾股定理的知识.(1)作CH⊥AD于点H.在Rt△ACH中,根据三角函数可求AH= ,CH=
,CH=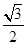 .从而得到HD=1.3.再根据勾股定理得到CD的高.
.从而得到HD=1.3.再根据勾股定理得到CD的高.
(2)同(1)可得,AH=acos ,CH=asin
,CH=asin .从而得到HD=b﹣acos
.从而得到HD=b﹣acos .再根据勾股定理得到CD的高.
.再根据勾股定理得到CD的高.

在Rt△ACH中,∵AC=1,∠CAH=60°,
∴AH=
 ,CH=
,CH=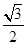 .
.∵AD=1.8,
∴HD=1.3.
∴CD=
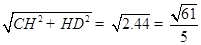 (m);
(m);(2)同上可得,AH=acos
 ,CH=asin
,CH=asin .
.∵AD=b,
∴HD=b﹣acos
 .
.∴CD=
 .
.考查了解直角三角形的应用,本题关键是熟悉三角函数、勾股定理的知识.(1)作CH⊥AD于点H.在Rt△ACH中,根据三角函数可求AH=
 ,CH=
,CH=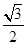 .从而得到HD=1.3.再根据勾股定理得到CD的高.
.从而得到HD=1.3.再根据勾股定理得到CD的高.(2)同(1)可得,AH=acos
 ,CH=asin
,CH=asin .从而得到HD=b﹣acos
.从而得到HD=b﹣acos .再根据勾股定理得到CD的高.
.再根据勾股定理得到CD的高.
练习册系列答案
相关题目
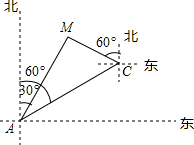
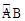 上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N. 时,求
时,求 的值;
的值;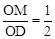 时,求y关于x 的函数解析式,并写出它的定义域;
时,求y关于x 的函数解析式,并写出它的定义域;
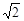 ≈1.414,
≈1.414,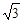 ≈1.732)
≈1.732)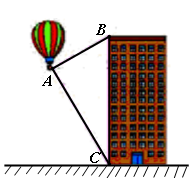
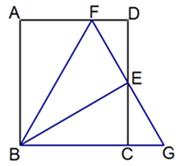
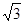 ,S△CGE=6
,S△CGE=6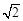 ≈1.414,
≈1.414,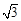 ≈1.732,
≈1.732,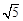 ≈2.236,
≈2.236,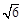 ≈2.449)
≈2.449) .
.
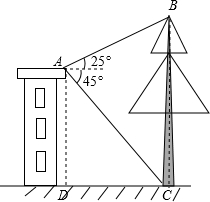
 -
- =________.
=________.