题目内容
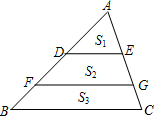如图，D、E、F、G是△ABC边上的点，且DE∥FG∥BC，DE，FG将△ABC分成三个部分，它们的面积比为S1：S2：S3=1：2：3，那么DE：FG：BC=________．
1：
：
分析：首先由DE∥FG∥BC，得到△ADE∽△AFG∽△ABC；因为相似三角形的面积比等于相似比的平方，以求得各三角形的对应边的比．
解答：∵DE∥FG∥BC，
∴△ADE∽△AFG∽△ABC，
∴
，
，
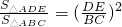∵S△AFG=S1+S2，S△ABC=S1+S2+S3，
∵S1：S2：S3=1：2：3，
∴=
，=
，
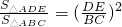∴DE：FG=1：，DE：BC=1：，
∴DE：FG：BC=1：：．
故答案为：1：：．
点评：此题考查了相似三角形的判定与性质．解题时要注意相似三角形的面积比等于相似比的平方．解题的关键是数形结合思想的合理应用．
：分析：首先由DE∥FG∥BC，得到△ADE∽△AFG∽△ABC；因为相似三角形的面积比等于相似比的平方，以求得各三角形的对应边的比．
解答：∵DE∥FG∥BC，
∴△ADE∽△AFG∽△ABC，
∴
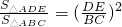，，∵S△AFG=S1+S2，S△ABC=S1+S2+S3，
∵S1：S2：S3=1：2：3，
∴
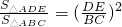=，=，∴DE：FG=1：
，DE：BC=1：，∴DE：FG：BC=1：
：．故答案为：1：
：．点评：此题考查了相似三角形的判定与性质．解题时要注意相似三角形的面积比等于相似比的平方．解题的关键是数形结合思想的合理应用．
练习册系列答案
相关题目
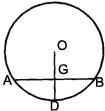14、如图，已知⊙P的半径OD=5，OD⊥AB，垂足是G，OG=3，则弦AB=
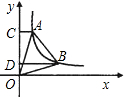如图，已知A，B两点是反比例函数y=
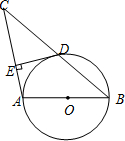如图AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC于点E．