题目内容
【题目】在平面直角坐标系xOy中，二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，则下列结论正确的是（ ）
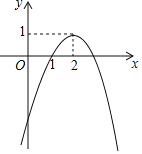
A.b2﹣4ac＜0
B.2a+b＝0
C.a+b+c＜0
D.关于x的方程ax2+bx+c＝﹣1有两个不相等的实数根
【答案】D
【解析】
根据函数图像与
轴的交点情况判定b2﹣4ac正负、二次函数的对称轴判定2a+b的值、当x＝1时判定a+b+c正负、ax2+bx+c＝﹣1的根转化为函数y＝ax2+bx+c与函数y＝﹣1图像交点的横坐标，依次判断即可．
解：A选项函数与x轴有两个交点故b2﹣4ac
0，故A选项错误，不符合题意；
B选项函数的对称轴为：x＝
＝2，即4a+ b＝0，故B选项错误，不符合题意；
C选项当x＝1时，y＝a+b+c＝0，故C选项错误，不符合题意；
D选项由图象得，函数y＝ax2+bx+c与函数y＝﹣1有两个交点，故关于x的方程ax2+bx+c＝﹣1有两个不相等的实数根，D选项正确，符合题意；
故选：D．
练习册系列答案
相关题目
【题目】某班级从甲、乙两位同学中选派一人参加知识竞赛，老师对他们的五次模拟成绩（单位：分）进行了整理，并计算出甲成绩的平均数是80分，甲、乙成绩的方差分别是320，40，但绘制的统计图表尚不完整．
甲、乙两人模拟成绩统计表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲成绩 | 90 | 100 | 90 | 50 |
|
乙成绩 | 80 | 70 | 80 | 90 | 80 |
甲、乙两人模拟成绩折线图
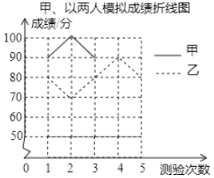
根据以上信息，请你解答下列问题：
（1）
（2）请完成图中表示甲成绩变化情况的折线；
（3）求乙成绩的平均数；
（4）从平均数和方差的角度分析，谁将被选中．
