题目内容
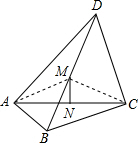
如图，在四边形ABCD中，AB=5，AD=AC=12，∠BAD=∠BCD=90°，M、N分别是对角线BD、AC的中点，则MN=______．
连接AM和CM
∵∠BAD=90°，AB=5，AD=12，
∴BD=
=13，
∵∠BAD=∠BCD=90°，点M是BD的中点，
∴AM=CM=
BD=
，
∵点N是AC的中点，
∴MN⊥AC，AN=CN=
AC=6，
在Rt△AMN中，MN=
=2.5，
故应填2.5．
∵∠BAD=90°，AB=5，AD=12，
∴BD=
| 52+122 |
∵∠BAD=∠BCD=90°，点M是BD的中点，
∴AM=CM=
| 1 |
| 2 |
| 13 |
| 2 |
∵点N是AC的中点，
∴MN⊥AC，AN=CN=
| 1 |
| 2 |
在Rt△AMN中，MN=
(
|
故应填2.5．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
