题目内容
已知A、B两点在数轴上分别表示的数为m、n.
(1)对照数轴填写下表:
(2)若A、B两点的距离记为d,试问d与m、n有何数量关系?并用文字描述出来:
(3)若已知A、B两点在数轴上分别表示的数为x和-1,则A、B两点的距离d可表示为d:|x+1|,若d=3,求x.
(1)对照数轴填写下表:
| m | 3 | -3 | -3 | -3 | 2 | -1.5 |
| n | 1 | 0 | 1 | -1 | -3 | -1.5 |
| A、B两点的距离 | 2 | 3 | 4 | 2 | 5 | 0 |
(3)若已知A、B两点在数轴上分别表示的数为x和-1,则A、B两点的距离d可表示为d:|x+1|,若d=3,求x.
分析:(1)数轴上两点间的距离d等于表示两点数之差的绝对值,即d=|m-n|;
(2)根据(1)得出的结论列出含绝对值的一元一次方程,利用绝对值的代数意义化简即可求出x的值.
(2)根据(1)得出的结论列出含绝对值的一元一次方程,利用绝对值的代数意义化简即可求出x的值.
解答:解:(1)d=|m-n|,文字描述为:数轴上两点间的距离d等于表示两点数之差的绝对值;
(2)根据题意得:|x+1|=3,
可得x+1=3或x+1=-3,
解得:x=2或-4.
(2)根据题意得:|x+1|=3,
可得x+1=3或x+1=-3,
解得:x=2或-4.
点评:此题考查了数轴,弄清题意是解本题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

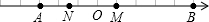
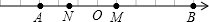
 如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)

 -
- +
+ +
+


 AB,试求点P所对应的数为多少?
AB,试求点P所对应的数为多少?