题目内容
 如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是
30
30
.(2)经过几秒,点M、点N分别到原点O的距离相等?
(3)当点M运动到什么位置时,恰好使AM=2BN?
分析:(1)根据点A表示的数为-10,OB=3OA,可得点B对应的数;
(2)分①点M、点N在点O两侧;②点M、点N重合两种情况讨论求解;
(3)①点N在点B左侧;②点N在点B右侧两种情况讨论求解.
(2)分①点M、点N在点O两侧;②点M、点N重合两种情况讨论求解;
(3)①点N在点B左侧;②点N在点B右侧两种情况讨论求解.
解答:解:(1)OB=3OA=30.
故B对应的数是30;
(2)设经过x秒,点M、点N分别到原点O的距离相等
①点M、点N在点O两侧,则
10-3x=2x,
解得x=2;
②点M、点N重合,则
3x-10=2x,
解得x=10.
所以经过2秒或10秒,点M、点N分别到原点O的距离相等;
(3)设经过y秒,恰好使AM=2BN.
①点N在点B左侧,则
3y=2(30-2y),
解得y=
,
3×
-10=
;
②点N在点B右侧,则
3y=2(2y-30),
解得y=60,
3×60-10=170;
即点M运动到
或170位置时,恰好使AM=2BN.
故答案为:30.
故B对应的数是30;
(2)设经过x秒,点M、点N分别到原点O的距离相等
①点M、点N在点O两侧,则
10-3x=2x,
解得x=2;
②点M、点N重合,则
3x-10=2x,
解得x=10.
所以经过2秒或10秒,点M、点N分别到原点O的距离相等;
(3)设经过y秒,恰好使AM=2BN.
①点N在点B左侧,则
3y=2(30-2y),
解得y=
| 60 |
| 7 |
3×
| 60 |
| 7 |
| 110 |
| 7 |
②点N在点B右侧,则
3y=2(2y-30),
解得y=60,
3×60-10=170;
即点M运动到
| 110 |
| 7 |
故答案为:30.
点评:此题主要考查了一元一方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
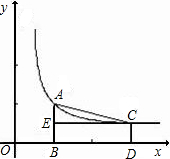 如图,已知A、C两点在双曲线y=
如图,已知A、C两点在双曲线y= (2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是
(2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是 如图,已知A、B两点的坐标分别为(
如图,已知A、B两点的坐标分别为( 如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.
如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论. 如图,已知E、F两点在线段BC上,AB=AC,BF=CE,你能判断线段AF和AE的大小关系吗?说明理由.
如图,已知E、F两点在线段BC上,AB=AC,BF=CE,你能判断线段AF和AE的大小关系吗?说明理由.