题目内容
【题目】如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1.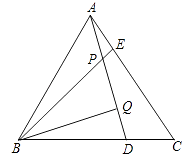
(1)求证:∠BPQ=60°(提示:利用三角形全等、外角的性质)
(2)求BE的长.
【答案】
(1)解:如图,
∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠ACD=60°,
又∵AE=CD,
∴△BAE≌△ACD,
∴∠1=∠2,
∵∠BAE=∠1+∠BAD=60°,
∴∠BAE=∠2+∠BAD=60°,
∴∠BPQ=60°
(2)解:∵BQ⊥AD,∴∠BQP=90°,又∵∠BPQ=60°,∴∠PBQ=30°,∴BP=2PQ=2×4=8,∴BE=BP+PE=8+1=9
【解析】(1)根据已知条件可证△BAE≌△ACD,结论可得证;(2)根据30°所对的直角边等于斜边的一半可求解。

练习册系列答案
相关题目