Question

如图，已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为h₁、h₂、h₃，△ABC的高为h．在图①中，点P是边BC的中点，由S_△ABP+S_△ACP=S_△ABC得，AB．h₁+AC．h₂=BC．h，可得h₁+h₂=h又因为h₃=0，所以：h₁+h₂+h₃=h．
图②～⑤中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）请探究：图②～⑤中，h₁、h₂、h₃、h之间的关系；（直接写出结论）
（2）说明图②所得结论为什么是正确的；
（3）说明图⑤所得结论为什么是正确的．

Answer 1

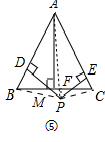解：（1）②h_l+h₂+h₃=h；③h₁-h₂+h₃=h；④h₁+h₂+h₃=h；⑤h₁+h₂-h₃=h．

（2）图②中，h₁+h₂+h₃=h．
连接AP，
则S_△APB+S_△APC=S_△ABC，
∴AB×h₁+AC×h₂=BC×h．
又h₃=0，AB=AC=BC，
∴h₁+h₂+h₃=h．

（3）图⑤中，h₁+h₂-h₃=h．
连接PA、PB、PC，（如答图）
则S_△APB+S_△APC=S_△ABC+S_△BPC．
∴AB×h_l+AC×h₂=BC×h+BC×h₃
又AB=AC=BC，
∴h₁+h₂=h+h₃．
∴h₁+h₂-h₃=h．
分析：（1）根据已知可以证得：②h_l+h₂+h₃=h；③h₁-h₂+h₃=h；④h₁+h₂+h₃=h；⑤h₁+h₂-h₃=h；
（2）连接AP，可得S_△APB+S_△APC=S_△ABC，由h₃=0，AB=AC=BC，即可证得h₁+h₂+h₃=h；
（3）连接PA、PB、PC，可得S_△APB+S_△APC=S_△ABC+S_△BPC，由AB=AC=BC，即可求得h₁+h₂=h+h₃，则可得h₁+h₂-h₃=h．
点评：此题考查了等边三角形的性质与三角形面积的求解方法．此题难度适中，解题的关键是注意数形结合思想的应用与辅助线的作法．