题目内容
 如图,△ABC在方格中.
如图,△ABC在方格中.
(1)请在方格纸上建立平面直角坐标系,使A(2,3)、C(5,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′.
解:(1)如图画出原点O,x轴、y轴,建立直角坐标系,

可知B的坐标为(2,1);
(2)如图,画出图形△A′B′C′.
分析:(1)根据已知点的坐标,建立平面直角坐标系,由坐标系确定B点坐标即可;
(2)连接OA并延长,在延长线上截取AA′=OA,BB′=OB,CC′=OC,连接A′B′,B′C′,A′C′,可得出满足题意的△A′B′C′.
点评:此题考查了作图-位似变换,画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.

可知B的坐标为(2,1);
(2)如图,画出图形△A′B′C′.
分析:(1)根据已知点的坐标,建立平面直角坐标系,由坐标系确定B点坐标即可;
(2)连接OA并延长,在延长线上截取AA′=OA,BB′=OB,CC′=OC,连接A′B′,B′C′,A′C′,可得出满足题意的△A′B′C′.
点评:此题考查了作图-位似变换,画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
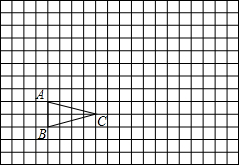 如图,△ABC在方格纸中
如图,△ABC在方格纸中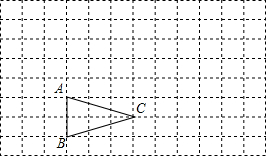 如图,△ABC在方格中.
如图,△ABC在方格中. 如图,△ABC在方格纸中
如图,△ABC在方格纸中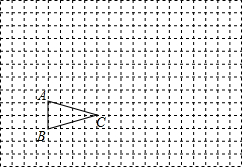 大后的位似图形△A′B′C′;
大后的位似图形△A′B′C′;