题目内容
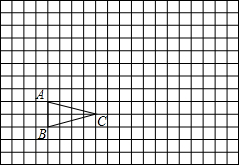 如图,△ABC在方格纸中
如图,△ABC在方格纸中(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.
分析:(1)A点的坐标为(2,3)所以原点O的坐标就在A点左2个格,下3个格的点上.由此建立直角坐标系,读出B点坐标;
(2)连接OA,OB,OC,并延长到OA′,OB′,OC′,使OA′,OB′,OC′的长度是OA,OB,OC的2倍.然后顺次连接三点;
(3)从网格上可看出三角形的底和高,利用三角形的面积公式计算.
(2)连接OA,OB,OC,并延长到OA′,OB′,OC′,使OA′,OB′,OC′的长度是OA,OB,OC的2倍.然后顺次连接三点;
(3)从网格上可看出三角形的底和高,利用三角形的面积公式计算.
解答: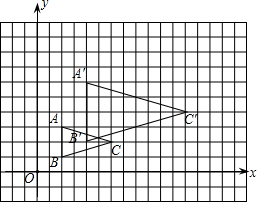 解:(1)画出原点O,x轴、y轴.(1分)B(2,1)(2分)
解:(1)画出原点O,x轴、y轴.(1分)B(2,1)(2分)
(2)画出图形△A′B′C′.(5分)
(3)S=
×4×8=16.(7分)
 解:(1)画出原点O,x轴、y轴.(1分)B(2,1)(2分)
解:(1)画出原点O,x轴、y轴.(1分)B(2,1)(2分)(2)画出图形△A′B′C′.(5分)
(3)S=
| 1 |
| 2 |
点评:本题综合考查了直角坐标系,位似图形,三角形的面积.

练习册系列答案
相关题目
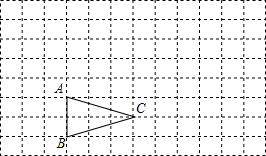 如图,△ABC在方格中.
如图,△ABC在方格中. 如图,△ABC在方格纸中
如图,△ABC在方格纸中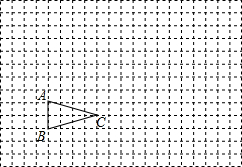 大后的位似图形△A′B′C′;
大后的位似图形△A′B′C′;