��Ŀ����
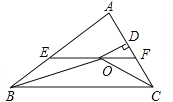
����Ŀ����ͼ���ı���ABCD�Ǿ���ֽƬ��AB=2�����۾���ֽƬABCD��ʹAD��BC�غϣ��ۺ�ΪEF��չƽ���ٹ���B�۵�����ֽƬ��ʹ��A����EF�ϵĵ�N���ۺ�BM��EF�ཻ�ڵ�Q���ٴ�չƽ������BN��MN���ӳ�MN��BC�ڵ�G�������½��ۣ�
�١�ABN=60�㣻��AM=1����QN= ![]() ���ܡ�BMG�ǵȱ������Σ���PΪ�߶�BM��һ���㣬H��BN���е㣬��PN+PH����Сֵ��
���ܡ�BMG�ǵȱ������Σ���PΪ�߶�BM��һ���㣬H��BN���е㣬��PN+PH����Сֵ�� ![]() ��
��
������ȷ���۵������ �� 
���𰸡��٢ܢ�
���������⣺��ͼ1������AN��
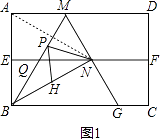
��EF��ֱƽ��AB��
��AN=BN��
�����۵������ʣ��ɵ�
AB=BN��
��AN=AB=BN��
���ABNΪ�ȱ������Σ�
���ABN=60�㣬��PBN=60���2=30�㣬
�����ۢ���ȷ��
�ߡ�ABN=60�㣬��ABM=��NBM��
���ABM=��NBM=60���2=30�㣬
��AM= ![]() ��
��
�����ۢڲ���ȷ��
��EF��BC��QN�ǡ�MBG����λ�ߣ�
��QN= ![]() BG��
BG��
��BG=BM= ![]() ��
��
��QN= ![]() ��
��
�����ۢ۲���ȷ��
�ߡ�ABM=��MBN=30�㣬��BNM=��BAM=90�㣬
���BMG=��BNM����MBN=90�㩁30��=60�㣬
���MBG=��ABG����ABM=90�㩁30��=60�㣬
���BGM=180�㩁60�㩁60��=60�㣬
���MBG=��BMG=��BGM=60�㣬
���BMGΪ�ȱ������Σ�
�����ۢ���ȷ��
�ߡ�BMG�ǵȱ������Σ���N��MG���е㣬
��BN��MG����BN=BGsin60��= ![]() ��
��
����������֪E���H�����BM�Գƣ���PH=PE��
��P��Q�غ�ʱ��PN+PH��ֵ��С����ʱPN+PH=PN+PE=EN��
��EN= ![]() =
= ![]() ��
��
��PN+PH= ![]() ��
��
��PN+PH����Сֵ�� ![]() ��
��
�����ۢ���ȷ��
���Դ��ǣ��٢ܢݣ�
�����㾫�������ڱ��⿼�����Գ�-���·�����⣬��Ҫ�˽���֪����㣬�����·������ȷ������෴����֪�յ��㣬�����·������֪�����յ㣬�������֮������·������ͼ���������·�����ܵó���ȷ�𰸣�