题目内容
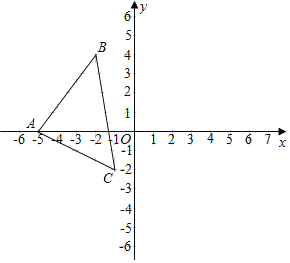
【题目】如图①,已知抛物线y=﹣x2﹣2x+3与x轴交于点A和点B,与y轴交于点C.
(1)直接写出A,B,C三点的坐标:A ;B ;C ;
(2)在该抛物线的对称轴上是否存在点P,时△APC的周长最小,若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图②,若点E为第二象限抛物线上的一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.

【答案】(1)A(1,0);B(﹣3,0);C(0,3);(2)存在.(3)点E坐标为(![]() ).
).
【解析】试题分析:
(1)在y=﹣x2﹣2x+3中分别由y=0和x=0求出对应的x的值和y的值即可得到A、B、C三点的坐标;
(2)由已知易得抛物线y=﹣x2﹣2x+3的对称轴为直线x=1,由题意可知点A、B关于直线x=1对称,连接BC交直线x=1于点P,则此时△ACP的周长最小,由点B、C的坐标可求出直线BC的解析式,把x=1代入所求解析式中求得对应的y的值即可得到点P的坐标;
(3)如图2,连接OE,由题意可设点E的坐标为(a,﹣a2﹣2a+3)(﹣3<a<0),由S四边形BOCE=S△OBE+S△OCE即可列式表达出其面积,将所得表达式配方,结合二次函数的性质即可得到四边形BOCE面积的最大值和对应的点E的坐标.
试题解析:
(1)令x=0得:y=3,
∴C(0,3).
令y=0,则0=﹣x2﹣2x+3,解得:x=﹣3或x=1,
∴A(1,0),B(﹣3,0).
故答案为:A(1,0);B(﹣3,0);C(0,3).
(2)存在.
如图①所示:连接BC,交抛物线的对称轴与点P,连接PA.
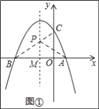
由题意可知,A、B两点关于抛物线的对称轴x=﹣1对称
∴PB=PA.
∴PC+PA=PC+PB.
由两点之间线段最短可知:PC+PA有最小值.
∴此时△APC周长最小.
设直线BC的解析式为y=kx+b.
将点B和点C的坐标代入得: ![]() ,解得k=1,b=3.
,解得k=1,b=3.
∴直线BC的解析式为y=x+3.
把x=﹣1代入y=x+3得y=2
∴P(﹣1,2)
(3)如图②所示:连接OE.
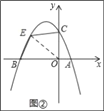
设E(a,﹣a2﹣2a+3)(﹣3<a<0).
S四边形BOCE=![]() OB|yE|+
OB|yE|+![]() OC|xE|=
OC|xE|=![]() ×3×(﹣a)+
×3×(﹣a)+![]() ×3×(﹣a2﹣2a+3)=﹣
×3×(﹣a2﹣2a+3)=﹣![]() a2﹣
a2﹣![]() a+
a+![]() =﹣
=﹣![]() (a+
(a+![]() )2+
)2+![]() .
.
∴当a=﹣![]() 时,四边形BOCE面积最大,且最大面积为
时,四边形BOCE面积最大,且最大面积为![]() .
.
此时,点E坐标为(![]() ).
).