题目内容
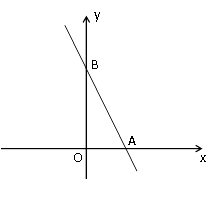
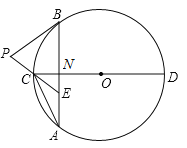
【题目】如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE.
(1)求证:AC2=AEAB;
(2)过点B作⊙O的切线交EC的延长线于点P,试判断PB与PE是否相等,并说明理由;
(3)设⊙O半径为4,点N为OC中点,点Q在⊙O上,求线段PQ的最小值.
【答案】(1)证明见解析;(2)PB=PE;(3)![]() .
.
【解析】
试题分析:(1)证明△AEC∽△ACB,列比例式可得结论;
(2)如图2,证明∠PEB=∠COB=∠PBN,根据等角对等边可得:PB=PE;
(3)如图3,先确定线段PQ的最小值时Q的位置:因为OQ为半径,是定值4,则PQ+OQ的值最小时,PQ最小,当P、Q、O三点共线时,PQ最小,先求AE的长,从而得PB的长,最后利用勾股定理求OP的长,与半径的差就是PQ的最小值.
试题解析:(1)如图1,连接BC,∵CD为⊙O的直径,AB⊥CD,∴![]() ,∴∠A=∠ABC,∵EC=AE,∴∠A=∠ACE,∴∠ABC=∠ACE,∵∠A=∠A,∴△AEC∽△ACB,∴
,∴∠A=∠ABC,∵EC=AE,∴∠A=∠ACE,∴∠ABC=∠ACE,∵∠A=∠A,∴△AEC∽△ACB,∴![]() ,∴AC2=AEAB;
,∴AC2=AEAB;
(2)PB=PE,理由是:
如图2,连接OB,∵PB为⊙O的切线,∴OB⊥PB,∴∠OBP=90°,∴∠PBN+∠OBN=90°,∵∠OBN+∠COB=90°,∴∠PBN=∠COB,∵∠PEB=∠A+∠ACE=2∠A,∠COB=2∠A,∴∠PEB=∠COB,∴∠PEB=∠PBN,∴PB=PE;
(3)如图3,∵N为OC的中点,∴ON=![]() OC=
OC=![]() OB,Rt△OBN中,∠OBN=30°,∴∠COB=60°,∵OC=OB,∴△OCB为等边三角形,∵Q为⊙O任意一点,连接PQ、OQ,因为OQ为半径,是定值4,则PQ+OQ的值最小时,PQ最小,当P、Q、O三点共线时,PQ最小,∴Q为OP与⊙O的交点时,PQ最小,∠A=
OB,Rt△OBN中,∠OBN=30°,∴∠COB=60°,∵OC=OB,∴△OCB为等边三角形,∵Q为⊙O任意一点,连接PQ、OQ,因为OQ为半径,是定值4,则PQ+OQ的值最小时,PQ最小,当P、Q、O三点共线时,PQ最小,∴Q为OP与⊙O的交点时,PQ最小,∠A=![]() ∠COB=30°,∴∠PEB=2∠A=60°,∠ABP=90°﹣30°=60°,∴△PBE是等边三角形,Rt△OBN中,BN=
∠COB=30°,∴∠PEB=2∠A=60°,∠ABP=90°﹣30°=60°,∴△PBE是等边三角形,Rt△OBN中,BN=![]() =
=![]() ,∴AB=2BN=
,∴AB=2BN=![]() ,设AE=x,则CE=x,EN=
,设AE=x,则CE=x,EN=![]() ﹣x,Rt△CNE中,
﹣x,Rt△CNE中,![]() ,x=
,x=![]() ,∴BE=PB=
,∴BE=PB=![]() =
=![]() ,Rt△OPB中,OP=
,Rt△OPB中,OP=![]() =
=![]() =
=![]() ,∴PQ=
,∴PQ=![]() ﹣4=
﹣4=![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案