题目内容
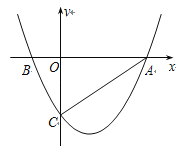
【题目】如图,在直角坐标系中,直线 ![]() 与x轴相交于点A,与y轴相交于点B.
与x轴相交于点A,与y轴相交于点B.
(1)直接写出A点的坐标;
(2)当x 时,y≤4;
(3)过B点作直线BP与x轴相交于P,若OP=2OA时,求ΔABP的面积。
(4)在y轴上是否存在E点,使得ΔABE为等腰三角形,若存在,直接写出满足条件的E点坐标.
【答案】
(1)解:A(2,0)
(2)≥ 0
(3)解:当P在A点右侧时,P(4,0)
![]()
![]()
当P在A点左侧时,P(-4,0)
![]()
![]()
![]()
(4)解: ![]()
【解析】(1)把y=0代入y = 2 x + 4中,解得x=2,所以A点的坐标为(2,0). 所以答案是A(2,0);
(2)把x=0代入y = 2 x + 4中,解得y=4,即直线 y = 2 x + 4与y轴的交点B的坐标为(4,0) ,由图象知,当x![]() 0时,y
0时,y![]() 4. 所以答案是为x
4. 所以答案是为x![]() 0;
0;
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小.

练习册系列答案
相关题目