ЬтФПФкШн
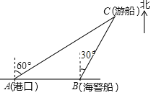
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§ЕФЭМЯѓЕФЖЅЕузјБъЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() гыИУЖўДЮКЏЪ§ЕФЭМЯѓНЛгк
гыИУЖўДЮКЏЪ§ЕФЭМЯѓНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЦфжаЕу
СНЕуЃЌЦфжаЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жсЩЯЃЎ
жсЩЯЃЎ![]() ЪЧ
ЪЧ![]() жсЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу
жсЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЗжБ№гыжБЯп
жсЕФДЙЯпЗжБ№гыжБЯп![]() КЭЖўДЮКЏЪ§ЕФЭМЯѓНЛгк
КЭЖўДЮКЏЪ§ЕФЭМЯѓНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЎ
СНЕуЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕМАетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЕФжЕМАетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕу![]() ЕФКсзјБъ
ЕФКсзјБъ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЧѓЯпЖЮ
ЪБЃЌЧѓЯпЖЮ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ4ЃЉШєжБЯп![]() гыЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсНЛЕуЮЊ
гыЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсНЛЕуЮЊ![]() ЃЌЮЪЪЧЗёДцдкЕу
ЃЌЮЪЪЧЗёДцдкЕу![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
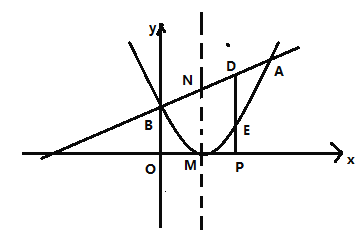
ЁОД№АИЁП(1)![]() ЃЌ
ЃЌ![]() ЃЛ(2)
ЃЛ(2)![]() ЃЛ(3) DEЕФзюДѓжЕЮЊ
ЃЛ(3) DEЕФзюДѓжЕЮЊ![]() ЃЛ(4)ДцдкЃЌЕу
ЃЛ(4)ДцдкЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() Лђ(
Лђ(![]() )Лђ(
)Лђ(![]() ЃЌ0)
ЃЌ0)
ЁОНтЮіЁП
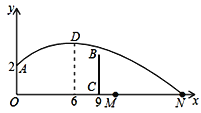
(1)ИљОнжБЯп![]() ОЙ§ЕуA(3ЃЌ4)ЧѓЕУm=1ЃЌИљОнЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕузјБъЮЊM(1ЃЌ0)ЃЌЧвОЙ§ЕуA(3ЃЌ4)МДПЩЧѓНтЃЛ
ОЙ§ЕуA(3ЃЌ4)ЧѓЕУm=1ЃЌИљОнЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕузјБъЮЊM(1ЃЌ0)ЃЌЧвОЙ§ЕуA(3ЃЌ4)МДПЩЧѓНтЃЛ
(2)ЯШЧѓЕУЕу![]() ЕФзјБъЃЌЕуDЕФзјБъЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНМДПЩЧѓНтЃЛ
ЕФзјБъЃЌЕуDЕФзјБъЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНМДПЩЧѓНтЃЛ
(3)гЩЬтвтЕУ![]() ЃЌдђ
ЃЌдђ![]() ИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓНтЃЛ
ИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓНтЃЛ
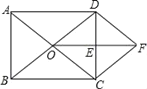
(4)ЗжСНжжЧщПіЃКDЕудкEЕуЕФЩЯЗНЁЂDЕудкEЕуЕФЯТЗНЃЌЗжБ№ЧѓНтМДПЩЃЎ
(1)ЁпжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕузјБъЮЊ![]() ЃЌ
ЃЌ
ЁрЩшЖўДЮКЏЪ§ЕФНтЮіЪНЮЊЃК![]()
ЁпХзЮяЯпОЙ§![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрЖўДЮКЏЪ§ЕФНтЮіЪНЮЊЃК![]() ЃЛ
ЃЛ
(2)Аб![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ
Аб![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]() ЃЌ
ЃЌ
ЁрЕуDЕФзјБъЮЊ(2ЃЌ3)ЃЌ
Ёр![]() ЃЌ
ЃЌ

Ёр![]() ЃЛ
ЃЛ
(3)гЩЬтвтЕУ![]() ЃЌ
ЃЌ
Ёр![]()
![]() ЁрЕБ
ЁрЕБ![]() (Ъєгк
(Ъєгк![]() ЗЖЮЇ)ЪБЃЌDEЕФзюДѓжЕЮЊ
ЗЖЮЇ)ЪБЃЌDEЕФзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
(4) ТњзуЬтвтЕФЕуPЪЧДцдкЕФЃЌРэгЩШчЯТЃК
ЁпжБЯпABЃК![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЁрЕуNЕФзјБъЮЊ(1ЃЌ2)ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпвЊЪЙЫФБпаЮЮЊЦНааЫФБпаЮжЛвЊ![]() ЃЌ
ЃЌ
ЁрЗжСНжжЧщПіЃК
ЂйDЕудкEЕуЕФЩЯЗНЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() (ЩсШЅ)Лђ
(ЩсШЅ)Лђ![]() ЃЛ
ЃЛ
ЂкDЕудкEЕуЕФЯТЗНЃЌдђ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() Лђ
Лђ![]()
злЩЯЫљЪіЃЌТњзуЬтвтЕФЕуPЪЧДцдкЕФЃЌЕуPЕФзјБъЮЊ![]() Лђ(
Лђ(![]() )Лђ(
)Лђ(![]() ЃЌ0) ЃЎ
ЃЌ0) ЃЎ

 РјдХЪщвЕЪюМйЯЮНгФўВЈГіАцЩчЯЕСаД№АИ
РјдХЪщвЕЪюМйЯЮНгФўВЈГіАцЩчЯЕСаД№АИЁОЬтФПЁПвбжЊ![]() ЪЧ
ЪЧ![]() ЕФЗДБШР§КЏЪ§ЃЌЯТБэИјГіСЫ
ЕФЗДБШР§КЏЪ§ЃЌЯТБэИјГіСЫ![]() гы
гы![]() ЕФвЛаЉжЕЃЎ
ЕФвЛаЉжЕЃЎ
| Ё | -4 | -2 | -1 | 1 | 3 | 4 | Ё | ||
| Ё | -2 | 6 | 3 | Ё |
ЃЈ1ЃЉЧѓГіетИіЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉИљОнКЏЪ§БэДяЪНЭъГЩЩЯБэЃЛ
ЃЈ3ЃЉИљОнЩЯБэЃЌдкЯТЭМЕФЦНУцжБНЧзјБъЯЕжазїГіетИіЗДБШР§КЏЪ§ЕФЭМЯѓЃЎ