题目内容
(1)如图1,在△ABC中,∠B、∠C均为锐角,其对边分别为b、c,求证:| b |
| sinB |
| c |
| sinC |
(2)在△ABC中,AB=
| 3 |
| 2 |
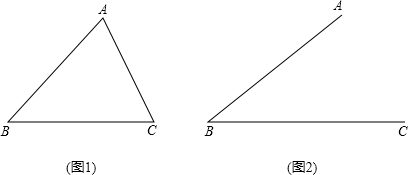
分析:(1)通过在BC边上作高,利用两个直角三角形和三角函数来求证.
(2)已知∠B=45°,则我们可以推测有两种情况,即锐角和钝角两种,按此思路来进行验证.
(2)已知∠B=45°,则我们可以推测有两种情况,即锐角和钝角两种,按此思路来进行验证.
解答: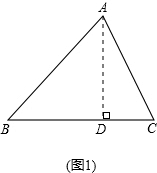 (1)证明:过A作AD⊥BC,垂足为D,
(1)证明:过A作AD⊥BC,垂足为D,
在Rt△ABD中,AD=csinB,
在Rt△ACD中,AD=bsinC,
csinB=bsinC,
故
=
.
(2)解:满足条件的△ABC有两个.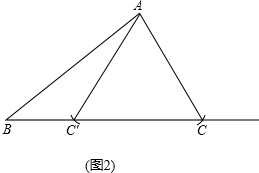
若∠ACB为锐角,由(1)的结论有
=
,
∴sinc=
,
∴∠ACB=60°;
若∠AC′C=∠ACC′=60°,
∴∠AC′B=120°.
 (1)证明:过A作AD⊥BC,垂足为D,
(1)证明:过A作AD⊥BC,垂足为D,在Rt△ABD中,AD=csinB,
在Rt△ACD中,AD=bsinC,
csinB=bsinC,
故
| b |
| sinB |
| c |
| sinc |
(2)解:满足条件的△ABC有两个.

若∠ACB为锐角,由(1)的结论有
| ||
| sin45° |
| ||
| sinc |
∴sinc=
| ||
| 2 |
∴∠ACB=60°;
若∠AC′C=∠ACC′=60°,
∴∠AC′B=120°.
点评:此题考查了辅助线的添法,验证法及直角三角形的性质和三角函数的综合运用.

练习册系列答案
相关题目



 图2,中间会出现一个小孔,如果正方形ABCD的边长为a,试计算图2中小孔的面积.
图2,中间会出现一个小孔,如果正方形ABCD的边长为a,试计算图2中小孔的面积.