题目内容
如图,在□ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)试说明:AB=CF;
(2)连接DE,若AD=2AB,试说明:DE⊥AF.

(1)试说明:AB=CF;
(2)连接DE,若AD=2AB,试说明:DE⊥AF.
(1)根据平行四边形的性质可得AB∥CD,AB=CD,根据平行线的性质可得∠B=∠BCF,由E是BC的中点可得BE=CE,再结合对顶角相等可证得△ABE≌△FCE,问题得证;
(2)由AB=CD,AB=CF结合AD=2AB可证得AD=DF,再根据等腰三角形的性质即可作出判断.
(2)由AB=CD,AB=CF结合AD=2AB可证得AD=DF,再根据等腰三角形的性质即可作出判断.
试题分析:
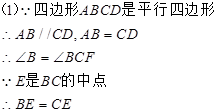
又∵∠AEB=∠FEC
∴△
|
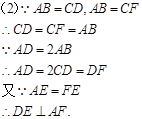
点评:平行四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
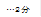
 的平分线
的平分线 交边
交边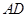 于
于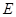 ,
, 的平分线
的平分线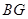 交
交 ,交
,交 .
.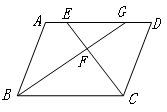

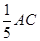 ,连接DE并延长交AB于M,连接BF交CD于N,
,连接DE并延长交AB于M,连接BF交CD于N,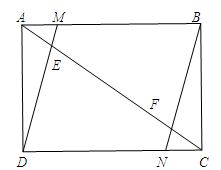
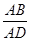 的值.
的值.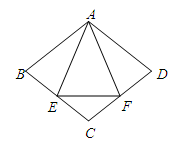
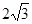 cm B.
cm B.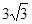 cm
cm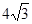 cm D.3 cm
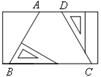
cm D.3 cm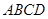 的位置如图所示,点
的位置如图所示,点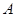 的坐标为
的坐标为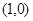 ,点
,点 的坐标为
的坐标为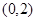 ;延长
;延长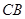 交
交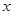 轴于点
轴于点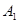 ,作正方形
,作正方形 ;延长
;延长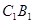 交
交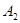 ,作正方形
,作正方形 …;按这样的规律进行下去,第
…;按这样的规律进行下去,第 个正方形的面积为
个正方形的面积为