题目内容
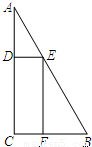
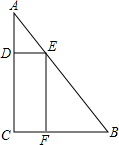 一块三角形废料如图所示,∠A=30°,∠C=90°,AB=6米.用这块废料剪出一个矩形CDEF,其中点D、E、F分别在AC、AB、BC上、设边AE的长为x米,矩形CDEF的面积为S平方米.
一块三角形废料如图所示,∠A=30°,∠C=90°,AB=6米.用这块废料剪出一个矩形CDEF,其中点D、E、F分别在AC、AB、BC上、设边AE的长为x米,矩形CDEF的面积为S平方米.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)根据(1)中的函数关系式,计算当x为何值时S最大,并求出最大值.
参考公式:二次函数y=ax2+bx+c(a≠0),当x=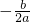 时,y最大(小)值=
时,y最大(小)值= .
.
解:(1) ∵四边形DEFC是矩形,
∵四边形DEFC是矩形,
∴∠ADE=90°,
∵∠A=30°,
∴DE= AE,
AE,
∵AE=x,
∴DE= x,
x,
∴AD= x,
x,
同理在直角三角形ACB中,AC= =3
=3 米,
米,
∴DC=AC-AD=3 -
- x,
x,
∴S矩形DECF=DE•CD= x(3
x(3 -
- x)=-
x)=-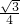 x2+
x2+ x,
x,
(2)∵S矩形DECF=-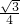 x2+
x2+ x,
x,
∴a=-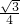 <0,
<0,
∴S有最大值,
∴x=- =3时,S最大=
=3时,S最大= =
=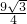 ,
,
∴当AB的长是3米时,矩形CDEF的面积最大,最大面积是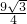 平方米.
平方米.
分析:(1)在直角三角形ADE中,利用直角三角形中30°的锐角所对的直角边是斜边的一半可求出DE的长,进而求出AD,同理在直角三角形ACB中可求出AC,所以就可以求出DC的长,即矩形DEFC的长,再利用矩形的面积公式即可得到S和x的函数关系式;
(2)利用求二次函数最值公式即可求出当x为何值时S最大,以及最大值.
点评:本题考查的是直角三角形的性质:在直角三角形ADE中,利用直角三角形中30°的锐角所对的直角边是斜边的一半以及勾股定理的运用,利用矩形的面积公式得到关于x的二次函数,根据二次函数的性质,确定x,y的取值和面积的最大值是解题的关键.
 ∵四边形DEFC是矩形,
∵四边形DEFC是矩形,∴∠ADE=90°,
∵∠A=30°,
∴DE=
 AE,
AE,∵AE=x,
∴DE=
 x,
x,∴AD=
 x,
x,同理在直角三角形ACB中,AC=
 =3
=3 米,
米,∴DC=AC-AD=3
 -
- x,
x,∴S矩形DECF=DE•CD=
 x(3
x(3 -
- x)=-
x)=-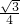 x2+
x2+ x,
x,(2)∵S矩形DECF=-
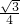 x2+
x2+ x,
x,∴a=-
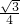 <0,
<0,∴S有最大值,
∴x=-
 =3时,S最大=
=3时,S最大= =
=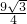 ,
,∴当AB的长是3米时,矩形CDEF的面积最大,最大面积是
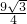 平方米.
平方米.分析:(1)在直角三角形ADE中,利用直角三角形中30°的锐角所对的直角边是斜边的一半可求出DE的长,进而求出AD,同理在直角三角形ACB中可求出AC,所以就可以求出DC的长,即矩形DEFC的长,再利用矩形的面积公式即可得到S和x的函数关系式;
(2)利用求二次函数最值公式即可求出当x为何值时S最大,以及最大值.
点评:本题考查的是直角三角形的性质:在直角三角形ADE中,利用直角三角形中30°的锐角所对的直角边是斜边的一半以及勾股定理的运用,利用矩形的面积公式得到关于x的二次函数,根据二次函数的性质,确定x,y的取值和面积的最大值是解题的关键.

练习册系列答案
相关题目
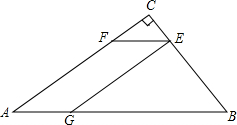 个平行四边形AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE=x
个平行四边形AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE=x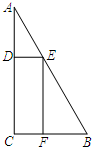 (2012•和平区一模)一块三角形废料如图所示,∠A=30°,∠C=90°,AB=12.用这块废料剪出一个矩形CDEF,其中,点D、E、F分别在AC、AB、BC上.要使剪出的矩形CDEF面积最大,点E应选在何处?
(2012•和平区一模)一块三角形废料如图所示,∠A=30°,∠C=90°,AB=12.用这块废料剪出一个矩形CDEF,其中,点D、E、F分别在AC、AB、BC上.要使剪出的矩形CDEF面积最大,点E应选在何处?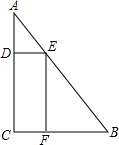 (2012•道外区二模)一块三角形废料如图所示,∠A=30°,∠C=90°,AB=6米.用这块废料剪出一个矩形CDEF,其中点D、E、F分别在AC、AB、BC上、设边AE的长为x米,矩形CDEF的面积为S平方米.
(2012•道外区二模)一块三角形废料如图所示,∠A=30°,∠C=90°,AB=6米.用这块废料剪出一个矩形CDEF,其中点D、E、F分别在AC、AB、BC上、设边AE的长为x米,矩形CDEF的面积为S平方米.