题目内容
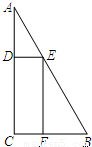
一块三角形废料如图所示,∠A=30°,∠C=90°,BC=6.用这块废料剪出一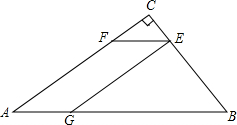 个平行四边形AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE=x
个平行四边形AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE=x(1)求x=2时,平行四边形AGEF的面积.
(2)当x为何值时,平行四边形AGEF的面积最大?最大面积是多少?
分析:设平行四边形AGEF的面积是S.利用平行四边形AGEF的对边互相平行知EF∥AG,所以同位角∠A=∠CFE=30°;然后在直角三角形ABC和直角三角形BEF中利用锐角三角函数的定义求得CF、AC的长度,从而求得平行四边形AGEF的底边AF=AC-CF;最后根据平行四边形的面积公式S=底×高得出关于S与x的函数关系式S=-
x2+6
x;
(1)将x=2代入S与x的函数关系式S=-
x2+6
x,并求解即可;
(2)利用配方法求二次函数的最值.
| 3 |
| 3 |
(1)将x=2代入S与x的函数关系式S=-
| 3 |
| 3 |
(2)利用配方法求二次函数的最值.
解答:解:设平行四边形AGEF的面积是S.
∵四边形AGEF是平行四边形,
∴EF∥AG;
∵∠A=30°,∠C=90°,CE=x,BC=6,
∴∠A=∠CFE=30°,
∴CF=
x,AC=6
,
∴AF=6
-
x;
∴S=AF•CE=(6
-
x)x=-
x2+6
x,即S=-
x2+6
x;
(1)当x=2时,S=-4
+12
=8
,即S=8
.
答:平行四边形AGEF的面积为8
(平方单位)…4分
(2)由S=-
x2+6
x,得
S=-
x2+6
x,
∴S=-
(x-3)2+9
,
∴当x=3时,平行四边形AGEF的面积最大,最大面积是9
(平方单位)…9分.
∵四边形AGEF是平行四边形,
∴EF∥AG;
∵∠A=30°,∠C=90°,CE=x,BC=6,
∴∠A=∠CFE=30°,
∴CF=
| 3 |
| 3 |
∴AF=6
| 3 |
| 3 |
∴S=AF•CE=(6
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
(1)当x=2时,S=-4
| 3 |
| 3 |
| 3 |
| 3 |
答:平行四边形AGEF的面积为8
| 3 |
(2)由S=-
| 3 |
| 3 |
S=-
| 3 |
| 3 |
∴S=-
| 3 |
| 3 |
∴当x=3时,平行四边形AGEF的面积最大,最大面积是9
| 3 |
点评:本题考查了平行四边形的性质、二次函数的最值.解答本题的关键是求出平行四边形AGEF的底边AF、底边上的高线CE的长度.

练习册系列答案
相关题目
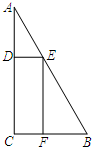 (2012•和平区一模)一块三角形废料如图所示,∠A=30°,∠C=90°,AB=12.用这块废料剪出一个矩形CDEF,其中,点D、E、F分别在AC、AB、BC上.要使剪出的矩形CDEF面积最大,点E应选在何处?
(2012•和平区一模)一块三角形废料如图所示,∠A=30°,∠C=90°,AB=12.用这块废料剪出一个矩形CDEF,其中,点D、E、F分别在AC、AB、BC上.要使剪出的矩形CDEF面积最大,点E应选在何处?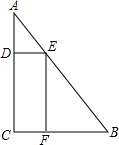 (2012•道外区二模)一块三角形废料如图所示,∠A=30°,∠C=90°,AB=6米.用这块废料剪出一个矩形CDEF,其中点D、E、F分别在AC、AB、BC上、设边AE的长为x米,矩形CDEF的面积为S平方米.
(2012•道外区二模)一块三角形废料如图所示,∠A=30°,∠C=90°,AB=6米.用这块废料剪出一个矩形CDEF,其中点D、E、F分别在AC、AB、BC上、设边AE的长为x米,矩形CDEF的面积为S平方米.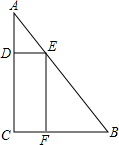 一块三角形废料如图所示,∠A=30°,∠C=90°,AB=6米.用这块废料剪出一个矩形CDEF,其中点D、E、F分别在AC、AB、BC上、设边AE的长为x米,矩形CDEF的面积为S平方米.
一块三角形废料如图所示,∠A=30°,∠C=90°,AB=6米.用这块废料剪出一个矩形CDEF,其中点D、E、F分别在AC、AB、BC上、设边AE的长为x米,矩形CDEF的面积为S平方米.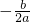 时,y最大(小)值=
时,y最大(小)值= .
.